Un peu de terminologie pour commencer :
- polygone convexe = enveloppe convexe d'un nombre fini de points dans $\mathbb{R}^2$,
- polyèdre convexe = enveloppe convexe d'un nombre fini de points dans $\mathbb{R}^3$,
- polytope convexe = enveloppe convexe d'un nombre fini de points dans $\mathbb{R}^d$.
Pour simplifier, je vais omettre le mot "convexe" et parler de polygone, polyèdre, polytope.
Les polyèdres apparaissent dans la nature, notamment dans la forme des cristaux, par exemple la pyrite est très cubique.
Source Wikimedia / Ivar Leidus
Polyèdres monumentaux : pyramides égyptiennes, environ 2600 avant J.C.
Les solides platoniciens¶
Une histoire qui remonte à l'antiquité, plusieurs siècles avant J.C.
tétrahèdre, cube, octahèdre, icosaèdre, dodécaèdre
Source Wikimedia / Drummyfish
En partie connus par Pythagore, ils apparaissent dans la philosophie de Platon, en association avec les éléments feu, terre, air, eau, ether.
Une description complète des solides platoniciens apparaît dans le dernier livre des Éléments d'Euclide.
Mysterium Cosmographicum¶
En 1596, Johannes Kepler publie un livre dans lequel il cherche à relier les 6 planètes connues et les solides platoniciens.
Mercure ☿, Vénus ♀, la Terre ⊕, Mars ♂, Jupiter ♃ et Saturne ♄
C'est un modèle sous forme de poupée russe 🪆. On emboîte les 5 solides :
octaèdre ⊂ icosaèdre ⊂ dodécaèdre ⊂ tétraèdre ⊂ cube,
en faisant se correspondre les sphères inscrite et circonscrite. On a donc 6 sphères (avec épaisseur).
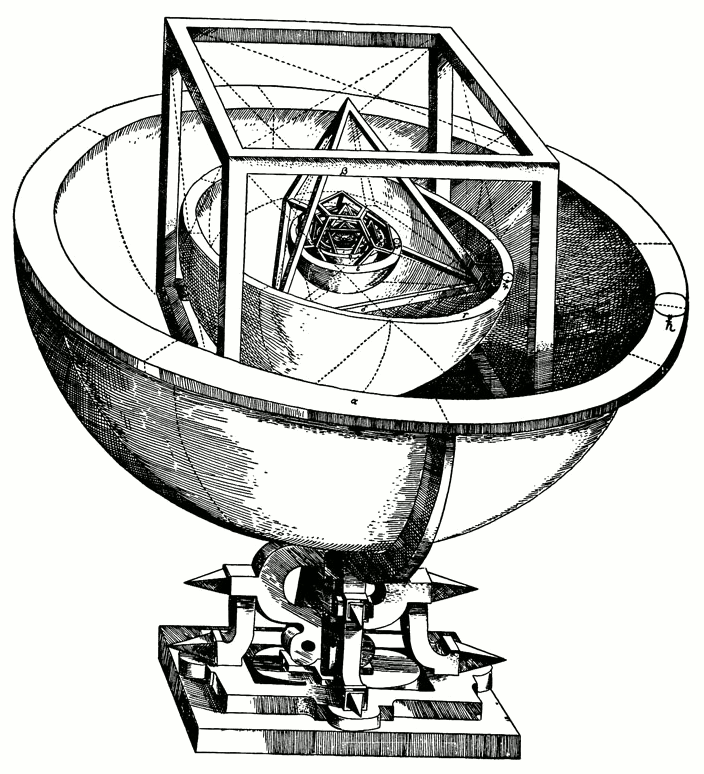
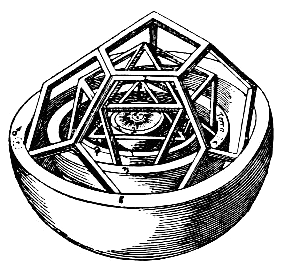Source Wikimedia / Johannes Kepler
C'était supposé expliquer les distances des planètes au soleil.
C'est un épisode intéressant dans l'histoire de l'astrophysique.
Dimensions supérieures¶
Le passage de la dimension 3 à la dimension 4 et plus attendra un bon moment, jusqu'au milieu du XIXe siècle.
Parmi les pionniers :
Alicia Boole Stott (1860-1940), Ludwig Schläfli (1814-1895), Pieter Schoute (1846-1913) et H. S. M. Coxeter (1907-2003).
Le terme de polytope est inventé par Reinhold Hoppe (1816-1900) en 1882.
Un jalon : la classification des polytopes réguliers en toute dimension, attribuée à Schläfli vers 1850, puis retrouvée par d'autres.
En dimension $4$, trois surprises : la 24-cellule, la 120-cellule et la 600-cellule.
Double description¶
Un polytope = enveloppe convexe d'un ensemble fini de points dans $\mathbb{R}^d$.
Autre définition équivalente = intersection bornée d'un nombre fini de demi-espaces dans $\mathbb{R}^d$.
On parle de double-description si on se donne les deux descriptions ; utile du point de vue algorithmique.
La conversion d'une description à l'autre nécessite un calcul.
De manière générale, l'étude des polytopes a mené à des algorithmes subtils.
Dualité¶
À chaque polytope $P$ dans $\mathbb{R}^d$, on peut associer un autre polytope $P^\star$ dans $\mathbb{R}^d$.
On suppose que le vecteur $0$ est dans l'intérieur de $P$. On note $\langle \,,\, \rangle$ le produit scalaire euclidien.
Alors $P^\star$ est l'ensemble des points $x$ tels que $\forall y \in P \quad \langle x,\,y \rangle \geq -1$.
Le polytope $P^\star$ est le polytope dual de $P$.
Dualité¶
La dualité est une involution (modulo dilatation globale).
Par exemple, le dual d'un polygone à $k$ sommets est un autre polygone à $k$ sommets,
Par exemple, le cube est le dual de l'octaèdre, le tétraèdre est auto-dual, le dodécaèdre est dual de l'icosaèdre.
Source Wikimedia / Watchduck
La dualité induit une bijection entre les faces de $P$ et celles de $P^\star$ en dimension complémentaire :
la "combinatoire" des faces est inchangée par dualité.
Les polytopes sont partout¶
La théorie des polytopes est un domaine en soi : la géométrie polyèdrale,
avec de nombreuses questions ouvertes.
Les polytopes sont utiles en mathématiques dans beaucoup de choses différentes :
optimisation linéaire : trouver le point maximisant une forme linéaire dans un polytope,
algèbre : axiomes qui s'écrivent comme des diagrammes commutatifs en forme de polytopes,
combinatoire : organisation "géométrique" d'ensembles combinatoires,
géometrie algébrique: théorie des variétés toriques, polytopes moments,
physique théorique : symétrie miroir via la dualité des polytopes : polytopes réflexifs.
Et cetera.
Polytopes à sommets entiers¶
La définition est claire : enveloppe convexe d'un ensemble fini de points dans $\mathbb{Z}^d$.
Par exemple, on peut prendre un hypercube en dimension $d$ : tous les points dont les coordonnées sont dans $\{0,1\}$.
Autres exemples : enveloppe convexe d'un sous-ensemble quelconque des sommets de cet hypercube.
Autre exemple : enveloppe convexe de toutes les permutations de $(1,2,\ldots,n)$ (permutoèdre).
L'icosaèdre et le dodécaèdre ont des coordonnées qui utilisent $\sqrt{5}$, donc ne sont pas à sommets entiers.
Il existe un modèle à sommets entiers de la 24-cellule en dimension 4.
Géométrie torique et variétés toriques¶
Toute une théorie qui établit un dictionnaire riche entre géométrie polyèdrale à sommets entiers et géométrie algébrique.
Très utile pour construire des variétés algébriques non triviales.
Ca permet de tester des conjectures générales de géométrie algébrique en disposant de méthodes plus combinatoires.
Idée générale :
Polytope à sommets entiers dans $\mathbb{Z}^d$ ➡️ éventail (union de cones) dans $\mathbb{Z}^d$
➡️ recollement d'ouverts dans $\mathbb{C}^d$ ➡️ variété algébrique de dimension $d$
Par exemple, le segment $[0,1]$ dans $\mathbb{Z}$ donne ainsi naissance à l'espace projectif $\mathbb{P}^1\mathbb{C}$ (sphère de Riemann).
Dualité des polytopes à sommets entiers¶
On prend $M \simeq \mathbb{Z}^d$ et $N \simeq \mathbb{Z}^d$ deux réseaux en dualité.
Si $P$ est un polytope à sommets dans $M$, contenant le vecteur $0$ dans son intérieur,
pour chaque face de $P$ de codimension $1$, on peut écrire une inégalité
sous la forme $ \langle x,\, v \rangle \geq -1$, quitte à dilater le vecteur $v$.
⚠️ En général, $v$ n'est pas dans le réseau dual $N$ !
Dualité des polytopes à sommets entiers¶
Contre-exemple : $P$ a pour sommets $(-1,-1), (1,-1), (-1,2), (1,1)$.
Alors $P$ est défini par les inégalités
$ x \geq -1, \quad y \geq -1, \quad x \leq 1, \quad x + 2 y \leq 3$,
et la dernière inégalité, une fois normalisée, est à coefficients rationnels.
Polytopes réflexifs¶
On dit qu'un polytope à sommets dans le réseau $M$ est réflexif si
il contient le point $0$ dans son intérieur,
ses inégalités s'écrivent $ \langle x,\, v \rangle \geq -1$ avec $v$ dans $N$ (i.e. à coefficients entiers).
Si $P$ est réflexif, son polytope dual $P^*$ est aussi réflexif.
Exemple : le carré de sommets $(-1,0), (1,0), (0,1), (0,-1)$.
Le dual est un carré de sommets $(-1,-1), (1,-1), (-1,1), (1,1)$.
Slogan : polytopes à sommets entiers dont le dual est aussi à sommets entiers !
Classification des polytopes réflexifs¶
On voudrait pouvoir classifier les polytopes réflexifs à changement de coordonnées près, i.e. modulo l'action de $\operatorname{GL}_d(\mathbb{Z})$.
Théorème (Lagarias / Ziegler 1991) : il y en a un nombre fini en chaque dimension.
Les compter est un problème très difficile : il y en a vraiment beaucoup !
En dimension 1 : juste le segment $[-1,1]$.
16 en dimension 2 : 
Classification des polytopes réflexifs¶
En dimension 3 : 4319 polytopes.
En dimension 4 : 473 800 776 polytopes (presque un demi-milliard).
En dimensions 3 et 4, la classification a été obtenue par les physiciens Maximilian Kreuzer (1960-2010) and Harald Skarke, en 1997,
dans un tour de force très impressionnant. Idées et algorithmes subtils, implémentation sophistiquée.
Motivés par la symétrie miroir des variétés Calabi-Yau (un peu plus dans un moment).
En dimension 5, aucun espoir. On estime vaguement que le nombre devrait avoir plusieurs dizaines de chiffres.
Un modèle pour la symétrie miroir¶
À chaque polytope réflexif $P$, la géométrie torique associe une variété algébrique $X_P$, qui peut être singulière.
Si elle est lisse, $X_P$ est une variété de Fano, et en prenant une hypersurface dans $X_P$, on obtient une variété Calabi-Yau $V_P$.
Les variétés Calabi-Yau intéressent les physiciens théoriciens : en théorie des cordes, ils cherchent un espace temps de la forme $\mathbb{R}^4 \times V$ et pour que la théorie marche bien, il faut que $V$ soit Calabi-Yau de dimension complexe $3$.
De plus, il existe des paires de familles de variétés Calabi-Yau qui donnent la même théorie physique.
On dit qu'elles sont reliées par la symétrie miroir, qui reste encore assez mystérieuse, même si les mathématiciens ont progressé.
Théorème de Batyrev¶
Victor Batyrev a montré en 1994 que si on prend deux polytopes réflexifs duaux l'un de l'autre, $P$ et $P^\star$,
alors les deux variétés Calabi-Yau $V_{P}$ et $V_{P^*}$ forment une paire liée par la symétrie miroir !
Ou du moins elles vérifient certaines prédictions de cette symétrie miroir.
C'est une source très importante d'exemples potentiels pour la symétrie miroir !
Pour la physique, on a besoin de variétés Calabi-Yau de dim. 3, donc de polytopes réflexifs en dim 4.
D'où les travaux de Kreuzer et Skarke sur le demi-milliard.
Construction de polytopes réflexifs¶
Pas tellement de constructions générales connues.
ensemble stable par dualité et par produit cartésien : P x P' en dimension la somme des dimensions,
une construction (#Flot) connue (Altmann, Hille, 1999), les polytopes de flots : à partir d'un graphe orienté sans cycle orienté,
une nouvelle construction (#Arb) : à partir d'un arbre enraciné avec chaque sommet décoré par un ensemble non vide.
Remarque : ces deux constructions ne permettent de construire qu'un tout petit pourcentage de polytopes réflexifs.
Remarque : la nouvelle construction #Arb est plus simple et plus "structurée" que la construction #Flot ;
Il reste à comprendre si ces deux constructions sont reliées entre elles. Il y a une intersection.
J'ai depuis généralisé un peu la construction #Arb, travail en cours.
Exemple pour la construction #Arb¶
Si on prend comme point de départ l'arbre décoré
avec la racine en haut,
alors les inégalités sont :
$a \geq 0,\quad b \geq 0,\quad c \geq 0,\quad d\geq 0\quad$ (coordonnées toutes positives)
et
$b \leq 2,\quad c + d \leq 3,\quad a + b + c +d \leq 5\quad$ (une inégalité par sommet de l'arbre)
ce qui définit (après translation) un polytope réflexif en dimension $4$ avec $14$ sommets et $84$ points entiers.
Le polytope réflexif dual a $8$ sommets et $9$ points entiers.
Conclusion¶
Les polytopes : une longue histoire et un sujet actif.
Les polytopes à sommets entiers : histoire plus récente, liens forts avec la géométrie algébrique, aspects algorithmiques
Les polytopes réflexifs : dualité subtile, liens avec la symétrie miroir.
Résultat récent : Une nouvelle construction de polytopes réflexifs, trouvée en étudiant autre chose !
Pour en savoir plus : Charles F. Doran et Ursula A. Whitcher, From Polygons to String Theory, Math. Mag. 85 (2012) 343-359.