Bi-associahedra by a general construction¶
Frédéric Chapoton, CNRS et université de Strasbourg
en collaboration avec Vincent Pilaud
aim: explain a general construction for polytopes called bi-associahedra, useful in algebraic topology
Associahedra
A sequence of polytopes $K_n$ for $n \geq 1$.
$K_n$ has dimension $n-1$ and stands for operations in $n+1$ arguments
Point, then segment, then pentagon, then ...

The associahedra $K_4$ of dimension 3, with 14 vertices, 21 edges, 3 rectangular faces and 6 pentagonal faces
and so on, one in every dimension
The associahedra first appeared
in the study of topological groups up to homotopy by Jim Stasheff (in 1963) and
in the works of Dov Tamari (1911-2006) about associativity (in 1951 Ph.D.).
not as polytopes but as cellular complexes.
Associahedra as polytopes
The associahedra were only later realized as polytopes, by Mark Haiman (in 1984) and Carl W. Lee (in 1989).
Now many different polytopal descriptions are known, by many people.
One turning point was the connection made by Sergey Fomin and Andrei Zelevinsky (in 2003) :
The vertex-edge graphs of associahedra are exchange graphs in cluster algebras of type $\mathbb{A}$.
This has increased the interest for associahedra, much beyond algebraic topology. Now even in mathematical physics.
Combinatorics : binary trees and rotation
Various ways to describe the vertices and faces of associahedra :
- vertices are binary trees, faces are planar trees
This is the best description for algebraic topology, related to axioms of $\mathbb{A}_{\infty}$-algebras (some details later)
- vertices are triangulations of a regular polygon, faces are dissections
This is the natural description when working with cluster algebras and cluster categories of Dynkin type $\mathbb{A}$.
Axioms of $\mathbb{A}_{\infty}$-algebras
The boundary of the associahedra $K_n$ is made of facets, each one being naturally
a product of two smaller associahedra $K_{p} \times K_{q}$ with $p+q = n$.
This leads to the axioms of $\mathbb{A}_{\infty}$-algebra on a chain complex, namely
- one operation $\mu_n$ with $n$ arguments for every $n \geq 2$ (think of $\mu_n$ as being the open cell in $K_{n-1}$)
such that (roughly and without signs)
- $d \circ \mu_n - \mu_n \circ d = \sum_{p + q = n + 1} \mu_{p} \circ \mu_{q}$
where $d$ is the differential.
Homotopy bialgebras and the bi-associahedra
$\mathbb{A}_{\infty}$-algebras describes associative algebras up-to-homotopy
meaning that one can transfer $\mathbb{A}_{\infty}$-algebras through quasi-isomorphisms of chain complexes
What about bialgebras ? structure with $m$ associative product and $\Delta$ associative coproduct, compatible
How to define $\mathbb{A}_{\infty}$-bialgebras and get a transfer theorem for them ?
There are some serious difficulties on the road : structure no longer described by an operad
This has been considered by Samson Saneblidze and Ronald Umble (2011) and Martin Markl (2015).
In their work, there appear new cellular complexes, bi-associahedra
combinatorics of bi-associahedra
Bi-associahedra are indexed by a pair of integers $(m,n)$ : $K_{m,n}$ of dimension $m+n-1$.
If $m=0$ or $n=0$, these are just associahedra, controlling homotopies for the product only or for the coproduct only.
First non-trivial example $K_{1,1}$ is a segment, controlling the homotopy between $\Delta \circ m \longleftrightarrow (m \otimes m) \circ (\Delta \otimes \Delta)$ which is the compatibility between product and coproduct
The vertices of $K_{m,n}$ are already quite complicated : bi-trees, one growing upward, one growing downward.
The polytope $K_{m,n}$ is the "unique homotopy" for operations with $m+1$ inputs and $n+1$ outputs.
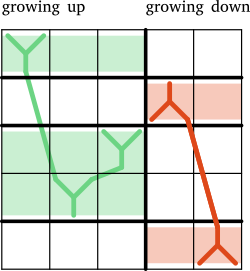
One typical bitree, corresponding to a vertex of $K_{3,2}$
4 inputs as leaves of the left tree
3 outputs as leaves of the right tree
facets of bi-associahedra
The next example after $K_{1,1}$ is $K_{2,1}$ which
is an hexagon.
Here comes the first obstruction to the definition of $\mathbb{A}_{\infty}$-bialgebras :
5 facets of $K_{2,1}$ are products of smaller $K_{i,j}$
BUT the sixth one is only a fiber-product of smaller $K_{i,j}$
Explicit issue
- start from $x \otimes y \otimes z$, apply $\Delta$ on each tensor factor
- get $x_1 \otimes x'_1 \otimes y_1 \otimes y'_1 \otimes z_1 \otimes z'_1$
- then either go to $(x_1 y_1) z_1\otimes (x'_1 y'_1) z'_1$ (left parentheses)
- or go to $x_1 (y_1 z_1)\otimes x'_1 (y'_1 z'_1)$ (right parentheses)
But there are two ways to go between these operations ! No canonical one.
This is getting worse in higher cases. Slightly horrible fiber products everywhere.👺
Construction of bi-associahedra
Our main result is the general construction of bi-associahedra as polytopes:
Theorem (C.-Pilaud) The polytopes defined as the shuffle of $K_n$ and $-K_m$ have the correct combinatorics, namely they are polytopal models for bi-associahedra $K_{m,n}$.
Here $-K_m$ is just an associahedra scaled by $-1$ (reversed).
So this looks simple : one just needs this shuffle operation !
What is it ? What objects can we shuffle ?
The generalized permutahedra
Classical permutahedra = convex hull of all permutations of $(0,1,\ldots,n-1)$ in $\mathbb{R}^n$.
Very classical and important polytope, related to the weak order on the symmetric group $\mathfrak{S}_n$
A generalized permutahedra is a polytope where one has moved parallely some facets of the classical permutohedra
For example, one can go from the regular hexagon to a pentagon (picture).
This familly can also be defined in terms of coarsening of fans.
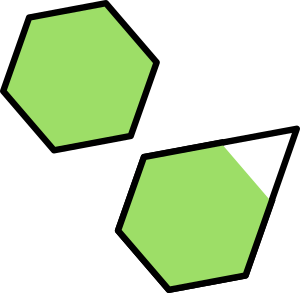
the permutohedra of dimension 2 as an hexagon
a generalized permutohedra obtained by removing one inequality
giving a pentagon
Associahedra are generalized permutahedra
One first needs to have associahedra in the shape of generalized permutohedra
They do exist. There are several of them in fact.
One possibility is to use Jean-Louis Loday's construction (2004), equivalent to the construction by truncations by Shlomo Sternberg and Steven Shnider (1993) (see cover of their book on quantum groups)
More generally, all polytopes for cambrian fans, defined in the context of cluster algebras, work.
The shuffle product
This has a rather simple definition ; produces a gen. permutohedra from any two generalized permutohedra.
If $P$ is a generalized permutohedra in $\mathbb{R}^m$
and $Q$ is a generalized permutohedra in $\mathbb{R}^n$
the $P \star Q = (P \times Q) + Z_{m,n} $
Here
$\times$ is the Cartesian product living in $\mathbb{R}^{m+n}$
$+$ stands for the Minkowski sum of polytopes
$Z_{m,n}$ is a special zonotope, itself a Minkowski sum of line segments.
Properties of the shuffle
This is an associative operation on the set of all generalized permutohedra.
This does not preserve the simple polytopes : some biassociahedra are not simple.
Merci !¶
- biassociahedra are polytopes ! complicated ones, related to homotopy bialgebras
- multiplihedra are special biassociahedra
- shuffle product $\star$ is a new operation
- shuffle can be used to construct many interesting polytopes
💎