Sur une combinatoire associée à chaque arbre d'ensembles

Frédéric Chapoton

C.N.R.S. et Université de Strasbourg

Séminaire Flajolet de Décembre 2024

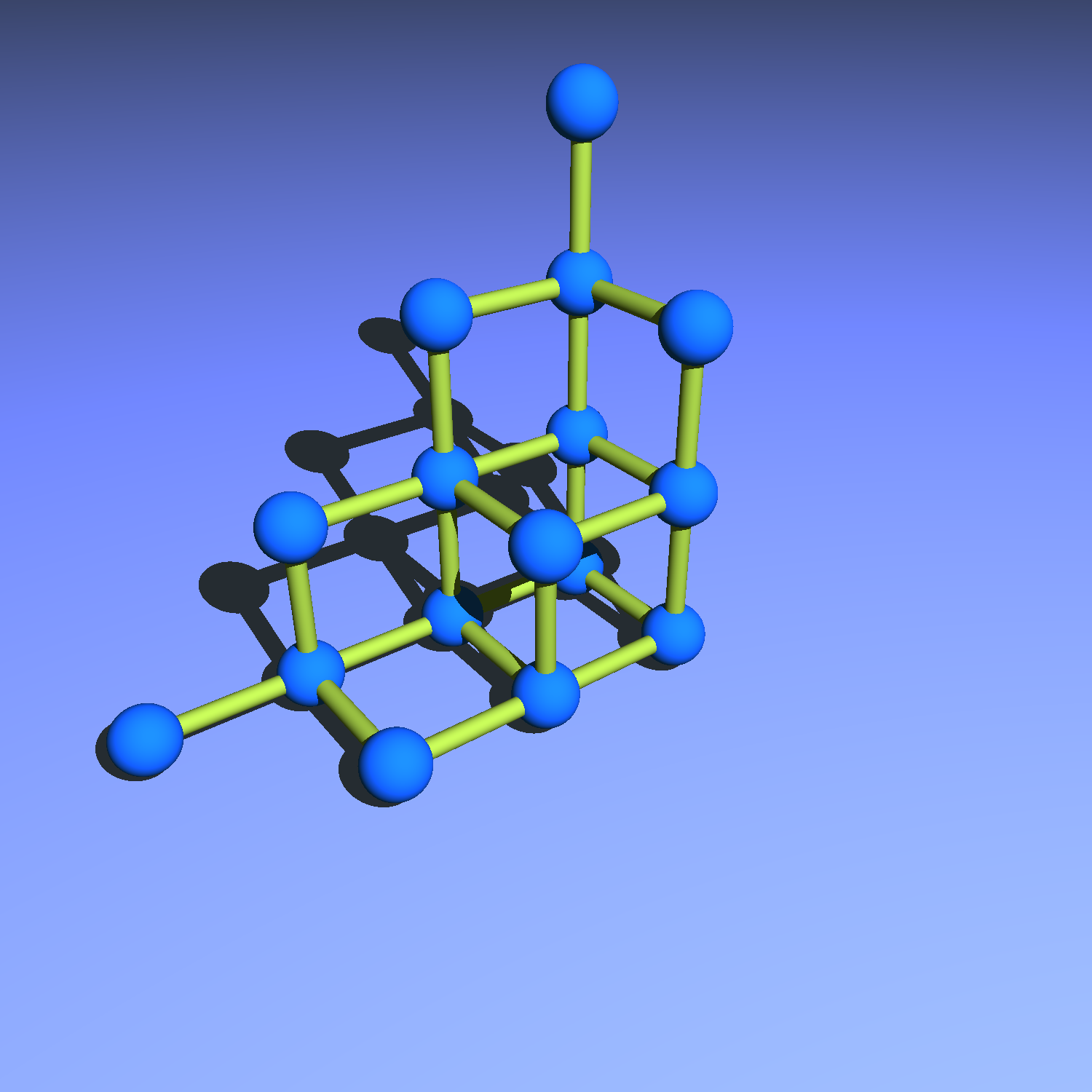
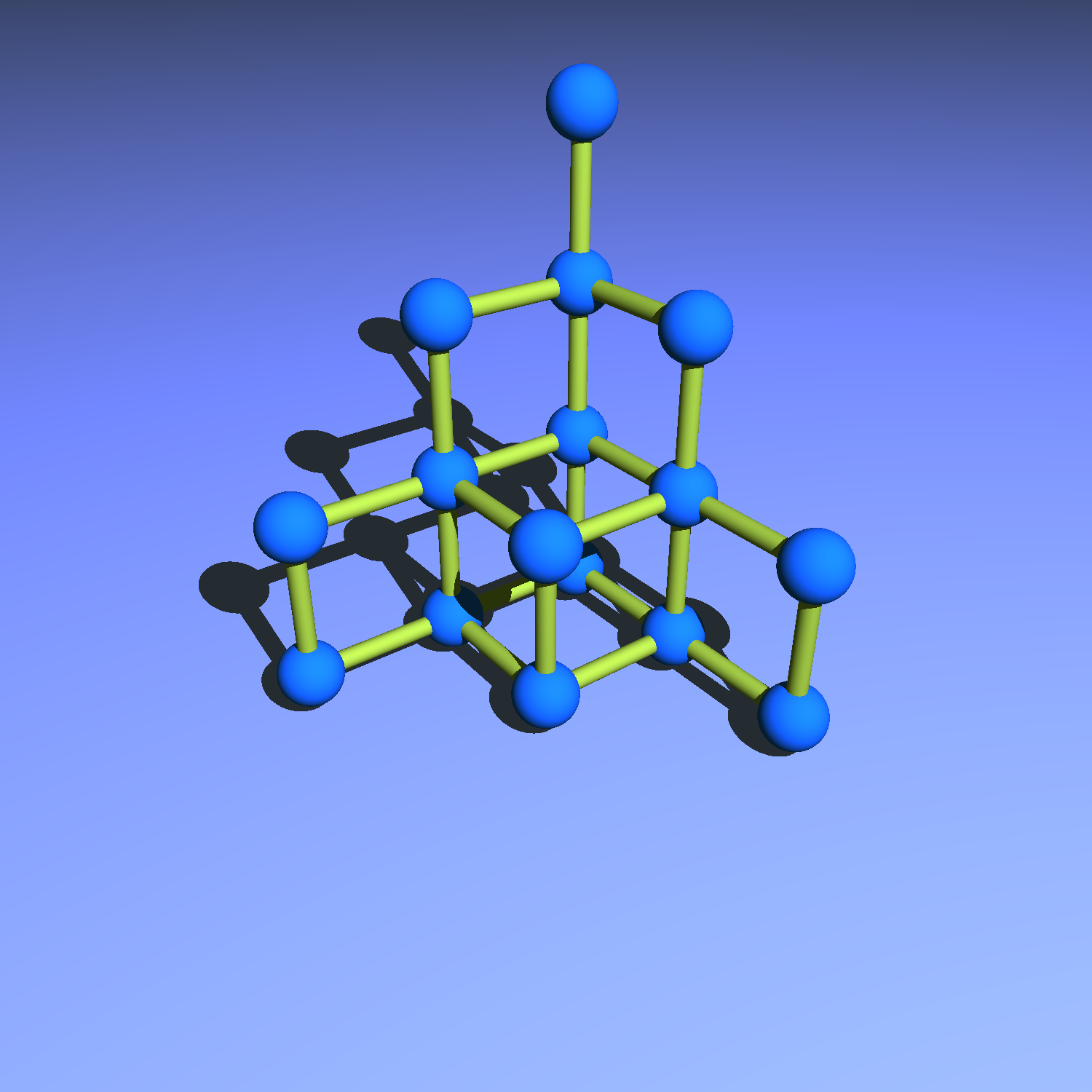
Des ordres partiels (posets) finis inclus dans $\mathbb{N}^n$ pour l'ordre composante par composante.

Les éléments sont les points entiers dans des polytopes.

Une sorte de nouveau champ, cousin inattendu de la combinatoire des amas, des treillis cambriens et des partitions non-croisées

🌳 arbres d'ensembles

Un tel poset est associé à chaque arbre d'ensembles.

Définition : un ensemble fini $I$, un arbre enraciné, dans chaque sommet de cet arbre une partie non-vide de $I$, les sommets forment une partition de $I$

En tant qu'espèce de structures : $R = \operatorname{Set}_{\geq 1} \times \operatorname{Set}(R)$

Par exemple, avec la racine en haut :

 ╭──{a,c}──╮
 │         │
{b}      ╭{h}╮
 │       │   │
{d}     {e} {f,g}
 │           │
{j}         {i}

💎 Le Polytope

On considère un arbre d'ensembles $t$ sur l'ensemble fini $I$. Dans $\mathbb{R}^I$, on a une coordonnée $x_i$ pour chaque élément $i$ de $I$.

À un sommet $v$ de $t$, on associe l'ensemble $N_v$ des éléments de $I$ dans ce sommet ou en dessous (dans un sous-arbre en dessous).

Alors on définit un polytope $Q_t$ par les inégalités $x_i \geq 0$ pour tout $i \in I$ et

$$\sum_{i \in N_v} x_i \leq |N_v|$$

pour tout sommet $v$.

Ceci définit un polytope à sommets entiers, simple et d'intérieur vide (sans point entier dans l'intérieur).

Un exemple de polytope

Prenons l'arbre d'ensembles

 ╭{a}╮
 │   │
{b} {c,d}

Alors (en notant $i$ pour $x_i$ pour simplifier) on a les inégalités

$$a \geq 0,\quad b \geq 0,\quad c \geq 0,\quad d \geq 0$$

et

$$a+b+c+d \leq 4,\quad b \leq 1 \quad \text{et}\quad c+d \leq 2.$$

Note : on a toujours l'inégalité : somme des coordonnées $\leq n$.

Le Poset

Une fois qu'on a défini le polytope $Q_t$, le poset $P_t$ est simple :

• les éléments sont les points entiers dans le polytope $Q_t$,

• la relation d'ordre est la comparaison terme à terme : $x\leq y$ si et seulement si $x_i \leq y_i$ pour tout $i \in I$.

Ça fait des posets gradués par la somme des coordonnées, avec un unique minimum $(0,0,\ldots,0)$ et plusieurs maxima.

Très cubique, visuellement. Couvertures = une coordonnée augmente de $1$.

🕵️ Pourquoi ?

L'histoire a commencé par une découverte fortuite dans le cas "Catalan" ou de type $\mathbb{A}$ que je vais expliquer tout de suite après.

Ensuite il y a eu un cas de type $\mathbb{B}$ au sens des groupes de Coxeter.

Et puis une relation avec les haloèdres, qui sont presque du type $\mathbb{D}$ mais pas vraiment.

Et puis une relation avec les polytopes de Hochschild. Et une autre relation avec certains polytopes de Stokes.

Cette construction avec les arbres d'ensembles unifie tout ça.

Le cas particulier "Catalan"

On regarde les arbres d'ensembles "linéaires" (dont chaque sommet a au plus un sous-arbre) avec un seul élément dans chaque sommet.

Si les coordonnées sont $x_1, \ldots, x_n$, alors

les inégalités sont $x_1 \leq 1$, $x_1+x_2 \leq 2$, ..., $x_1+x_2+\ldots+x_n \leq n$

qu'on reconnait comme la définition usuelle des fonctions de stationnement. (parking functions)

Donc le cardinal est bien un nombre de Catalan.

Ces posets semblent assez peu étudiés. Ils font partie des "Avalanche posets" de Combe-Giraudo.

M-triangles

Un petit rappel sur le $M$-triangle, polynôme générateur des nombres de Möbius, qui généralise le polynôme caractéristique.

Soit $P$ un poset gradué, alors le $M$-triangle de $P$ est le polynôme

$$M_P(X,Y) = \sum_{a\ \leq b} \mu_P(a,b) X^{|a|} Y^{|b|},$$

où $\mu_P$ est la fonction de Möbius et $|\cdot|$ est la graduation.

On note que la puissance de $Y$ est plus grande que celle de $X$ dans tous les monômes. D'où le nom triangle.

Par exemple, pour le poset des partitions non-croisées de $4$ points sur le cercle, ordonnées par raffinement, on trouve $$ \left(\begin{array}{rrrr} -5 & 10 & -6 & 1 \\ 10 & -16 & 6 & . \\ -6 & 6 & . & . \\ 1 & . & . & . \end{array}\right) $$ avec le terme constant en bas à gauche.

La diagonale énumère les éléments du poset selon leur graduation.

La colonne de gauche est le polynôme caractéristique.

Transmutation 🪄 des $M$-triangles

Introduisons une opération bizarre sur les $M$-triangles, la transmutation :

$$ \overline{m}(X,Y) = m\left(\frac{1-Y}{1-XY},1-XY\right).$$

C'est bien un polynôme. On vérifie facilement que c'est une involution.

Voici le $M$-triangle du poset $P_t$ pour le type "Catalan" de dimension $3$ : $$ \left(\begin{array}{rrrr} -1 & 6 & -10 & 5 \\ 3 & -8 & 5 & . \\ -3 & 3 & . & . \\ 1 & . & . & . \end{array}\right) \quad\text{dont le transmuté est}\quad \left(\begin{array}{rrrr} -5 & 10 & -6 & 1 \\ 10 & -16 & 6 & . \\ -6 & 6 & . & . \\ 1 & . & . & . \end{array}\right) $$

Vous reconnaissez quelque chose à droite ?

Transmutation avec les partitions non-croisées

C'est un énoncé général (découvert un peu par hasard) :

Le $M$-triangle du poset $P_t$ de type "Catalan" en dimension $n$ est le transmuté du $M$-triangle du poset des partitions non-croisées de $n+1$ éléments.

La preuve est un calcul qui n'explique rien.

Par ailleurs, ces deux posets ont le même polynôme Zêta, qui se factorise en facteurs de degré $1$ sur $\mathbb{Q}$.

La preuve est aussi un calcul.

Rappel : Le polynôme Zêta d'un poset a pour valeur en tout entier $N \geq 2$ le nombre de chaînes $a_{1} \leq \cdots \leq a_{N-1}$.

Le cas du type $\mathbb{B}$

Ici on regarde les arbres d'ensembles avec un seul sommet, qui contient $n$ éléments. (une patate 🥔)

Le polytope est particulièrement simple, une seule inégalité $x_1 + x_2 + \cdots + x_n \leq n$, en plus des $x_i \geq 0$, donc un simplexe. Le poset est très simple aussi.

Alors on a aussi les énoncés suivants :

Le $M$-triangle du poset $P_t$ de type $\mathbb{B}$ en dimension $n$ est le transmuté du $M$-triangle du poset des partitions non-croisées de type $\mathbb{B}_n$.

Par ailleurs, ces deux posets ont le même polynôme Zêta, qui se factorise en facteurs de degré $1$ sur $\mathbb{Q}$.

Encore une fois, une preuve calculatoire et pas éclairante.

Autres types de Coxeter

On pourrait espérer étendre ces relations aux autres types de groupes de Coxeter finis.

Ça ne marche pas très bien. On peut faire quelque chose en type $\mathbb{I}_2$, mais en sortant du cadre "arbres d'ensembles".

On ne trouve rien qui corresponde exactement par transmutation au type $\mathbb{D}$. Mais on trouve autre chose qui y ressemble beaucoup.

Si on cherche parmi les arbres d'ensembles ceux tels que le polynôme Zêta de $P_t$ se factorise totalement sur $\mathbb{Q}$, on observe $3$ familles infinies :

le type "Catalan" ou $\mathbb{A}$, le type $\mathbb{B}$ et le type "Haloèdre"

Les Haloèdres

C'est une famille de polytopes, cousins des associaèdres et des cycloèdres, un peu moins connus.

Un polytope simple en chaque dimension $n \geq 2$.

Les nombres de sommets sont $5, 16, 55, 196, 714, 2640, 9867, \ldots$

produit $c_{n-1} \times (3n-1)$ où $c_n$ est un nombre de Catalan, OEIS A051960

• une interprétation géométrique comme compactification d'un espace de module (Devadoss-Heath-Vipismakul)

• une définition combinatoire : les design-tubages du graphe cyclique. (Graph cubeahedra of cycle graph)

C'est une variation sur les graphe-associaèdres (tubes et tubages). Une des facettes est un cycloèdre.

Deux familles de type Haloèdre

Du coté des arbres d'ensembles, on peut regarder deux familles :

• un sommet racine contenant $n-1$ éléments + une feuille avec $1$ seul élément
• un sommet racine contenant $1$ élément + une feuille avec $n-1$ éléments

Proposition : Pour chacune de ces deux familles, le poset $P_t$ en dimension $n$ a autant d'éléments que l'haloèdre de dimension $n$.

Preuve par un petit calcul facile. Ça doit pouvoir se raffiner en une égalité de $h$-vecteurs.

Mais pourquoi cette coïncidence entre arbres d'ensembles différents ?

☯ Dualité Ehrhart-Zêta conjecturale

Soit $t$ un arbre d'ensembles linéaire (au plus un sous-arbre en chaque sommet, donc une unique feuille).

On peut définir un autre arbre d'ensembles linéaire $t'$ en échangeant les rôles de la racine et de la feuille (renversement haut-bas)

C'est clairement une involution.

Alors on a des relations assez surprenantes entre $t$ et $t'$.

Pour $t$ et $t'$ ainsi liés par renversement :

Conjecture

Si $Z_t$ est le polynôme Zêta du poset $P_t$ et $E_{t'}$ est le polynôme d'Ehrhart du polytope $Q_{t'}$,

alors $Z_t(u) = E_{t'}(u - 1)$.

Rappel : le polynôme d'Ehrhart en un entier $N$ compte les points entiers dans le polytope dilaté d'un facteur $N$.

Note : En particulier, $P_t$ et $P_{t'}$ ont le même cardinal (formule en $u=2$). En prenant les termes dominants, une égalité entre nombre de chaînes maximales du poset pour $t$ et volume du polytope pour $t'$. Explication par une triangulation unimodulaire ?

☯ Petit Exemple

En dimension 3, les deux familles de type haloèdre. Voir les deux images du début.

Prenons d'abord $t$ avec un racine de taille $2$ et une feuille de taille $1$. Cardinal $16$.

Alors $E_t(u) = \frac{1}{6} \cdot (u + 1) \cdot (19 u^2 + 23 u + 6)$ et donc $E_t(u-1) = \frac{1}{6} \cdot u \cdot (19 u^2 - 15 u + 2)$.

On a aussi $Z_t(u) = \frac{1}{3} \cdot u \cdot (2 u - 1) \cdot (5u - 2)$.

Prenons $t'$ avec une racine de taille $1$ et une feuille de taille $2$. Cardinal $16$.

Alors $E_{t'}(u)=\frac{1}{3} \cdot (u + 1) \cdot (2 u + 1) \cdot (5 u + 3)$ et donc $E_{t'}(u-1)=\frac{1}{3} \cdot u \cdot (2 u - 1) \cdot (5 u - 2)$.

On a aussi $Z_{t'}(u) = \frac{1}{6} \cdot u \cdot (19 u^2 - 15 u + 2)$.

🌳 Récurrence par sous-arbres

Plusieurs invariants (cardinal, volume, polynôme Zêta, polynôme d'Ehrhart, $M$-triangle) peuvent se calculer par récurrence en utilisant la structure d'arbre (racine + sous-arbres).

Ça utilise une projection entre polytopes de $Q_t$ vers un produit, dont on comprend bien les fibres.

Il faut souvent raffiner ces invariants selon la hauteur (somme des coordonnées) pour pouvoir obtenir une récurrence.

Par exemple, pour calculer le volume, il faut calculer une fonction "volume par tranche", polynomiale par morceaux. C'est plus simple de calculer sa transformée de Laplace, qui est un polynôme en $1/s$ et $\exp(-s)$.

Moyen exemple (en symbolisant un sous-ensemble par son cardinal)

╭3╮
│ │
1 1
  │
  4

Alors on a affaire à un polytope $Q_t$ en dimension $9$ avec $19990$ points entiers. Son volume est $60976/189$. Son polynôme d'Ehrhart est $$ \frac{1}{1890} \cdot (2 u + 1) \cdot (4 u + 1) \cdot (4 u + 3) \cdot (u + 1)^2 \cdot (19055 u^4 + 37538 u^3 + 25673 u^2 + 7059 u + 630). $$ Le poset $P_t$ a $19990$ éléments. Son polynôme Zêta est $$ \frac{1}{13440} \cdot u \cdot (3u - 2) \cdot (3u - 1) \cdot (542177u^{6} - 1508643u^{5} + 1676645u^{4} - 949045u^{3} + 285498u^{2} - 42152u + 2240). $$

Gros exemple

╭─┬1┬─╮
│ │ │ │
1 3 5 7

Un polytope en dimension $17$ ; le cardinal est $171531360$ et le polynôme d'Ehrhart est

$$\frac{(u + 1)^{4}}{2^{11} \cdot 3^4 \cdot 5} (3u + 1) \cdot (3u + 2) \cdot (5u + 1) \cdot (5u + 2) \cdot (5u + 3) \cdot (5u + 4) \\ \cdot (7u + 1) \cdot (7u + 2) \cdot (7u + 3) \cdot (7u + 4) \cdot (7u + 5) \cdot (7u + 6) \cdot (95u + 24) $$

On peut calculer ainsi facilement des exemples de taille relativement grande.

Bilan

D'un coté, un paysage riche de choses bien connues (combinatoire de Coxeter-Catalan et plus) :

• partitions non-croisées, treillis cambriens et amassés, posets semi-distributifs, polytopes simples et graphes d'échanges, éventails

Après transmutation, un nouveau monde

• des posets très cubiques, des arbres d'ensembles, des polytopes à sommets entiers sans points intérieurs, une dualité Ehrhart-Zêta

Plusieurs exemples de correspondances entre le paysage classique et le nouveau : type $\mathbb{A}$, type $\mathbb{B}$, haloèdres, posets de Hochschild (complexité minimale)

Une vaste famille encore à explorer : les arbres d'ensembles unaires-binaires et les polytopes de Stokes associés à certaines quadrangulations. Ceci ouvre une connexion avec les algèbres aimables et la théorie du tau-basculement.

🦊 Mais pourquoi ?

On a deux mondes et des coïncidences inexpliquées entre nombres ou polynômes de chaque coté.

Comment expliquer tout ca ? Pourquoi ?

Espoir : définir pour chaque arbre d'ensemble un treillis semi-distributif polytopal (une sorte de treillis alla Tamari)

Il faudrait que ce treillis ait le bon cardinal, et que les $M$-triangles des polytopes collent aussi.

On pourrait alors aussi demander une propriété sur le polynôme Zêta du treillis des tessons associé.

Omissions et oublis

La transmutation est une transposition des $H$-triangles.

Le $M$-triangle ressemble beaucoup au $F$-triangle du complexe d'amas.

Il semble que le $\Gamma$-triangle (après transmutation) soit toujours positif : une sphère simpliciale "flag" ?

Le cas des posets de Hochschild semble marcher très bien : transmutation des $M$-triangles et égalité des polynômes Zêta, à démontrer.

Dans le cas des haloèdres, on dispose du polytope, mais pas d'un bon poset semi-distributif. On a un début de piste.

Outre le $M$-triangle et le polynôme Zeta, coïncidence des coefficients dominants des $q$-polynômes Zêta.