Multiple zeta values and zinbiel algebras¶
Frédéric Chapoton
IRMA, CNRS et Université de Strasbourg
Septembre 2021
Preprint hal-03329815
Aim of the talk¶
Explain a proposal for new bases of the algebra of (motivic) multiple zeta values.
Main ingredient : zinbiel algebras and half-shuffle of iterated integrals.
First talk about multiple zeta values, then zinbiel algebras, then ...
Multiple zeta values (as real numbers)¶
A set of real numbers with a long history, going back to Euler, and a lot of connections with number theory (Riemann zeta function), knot theory (Drinfeld associator) and perturbative quantum field theory (Feynman integrals).
Consider the differential forms $\omega_0 = \frac{dt}{t}$ and $\omega_1 = \frac{dt}{1-t}$.
The multiple zeta values are the iterated integrals (à la Chen) of $\omega_0$ and $\omega_1$ on the real interval $[0,1]$ :
$$ I(\epsilon_1, \dots, \epsilon_k) = \mathop{\int\cdots\int}\limits_{0<t_1<\cdots <t_k<1} \omega_{\epsilon_1}(t_1) \cdots \omega_{\epsilon_k}(t_k) ,$$where each $\epsilon_i$ is either $0$ of $1$. To ensure convergence, one must assume $\epsilon_1=1$ and $\epsilon_k=0$.
These are real numbers, and in fact real periods, convergent integrals of algebraic differential forms (wedge product of rational 1-forms) over an algebraic domain (a simplex in the variables $t_i$)
Usually, one introduces another notation :
$$\zeta(k_1,\dots,k_r) = I(1,0^{k_1-1},1,0^{k_2-1},\dots,1,0^{k_r-1}),$$with the hypothesis $k_r \geq 2$. This integral is said to have weight $k_1+\dots+k_r$. The weight is the total number of $0$ and $1$.
The special case with a single $k \geq 2$ is exactly $\zeta(k)$, value of Riemann zeta function.
Easy claim : the $\mathbb{Q}$-linear span of all multiple zeta values forms an algebra over $\mathbb{Q}$.
Reason : much more generally, the product of iterated integrals is a sum of iterated integrals, sum over the shuffles of the differential forms. For example
$$I(a,b) I(\color{red}{C,D}) = I(a,b,\color{red}{C,D}) + I(a,\color{red}{C},b,\color{red}{D}) + \dots + I(\color{red}{C,D},a,b)$$where the sum is over all permutations of $\{a,b\} \cup \{\color{red}{C,D}\}$ in which the letters $a,b$ remain in their initial left-to-right order and the letters $C,D$ also.
Several famous facts and conjectures about this algebra :
The elements $\zeta(k_1,\dots,k_r)$ satisfy many relations. For example, already known to Euler, $\zeta(3) = \zeta(1,2)$, an instance of general duality relations. Another example : $3 \zeta(1,3) = \zeta(2,2)$.
Various sets of relations of different origins (double shuffle, associator, confluence). Some implications between them are known.
The algebra should be graded by the weight. No inhomogeneous relations.
The generating series of dimensions should be $1/(1-x^2-x^3)$ (Zagier).
The elements $\zeta(k_1,\dots,k_r)$ with all $k_i$ either $2$ or $3$ should form a basis (Hoffman).
All this has been tested, but not much is known. Closely related to hard questions of transcendance.
The algebra of motivic multiple zeta values¶
More abstract version, not made of real numbers, but more easy to prove things about.
This fits in the general setting of motives and abstract periods. One keyword is mixed Tate motives. No more details today.
Rough Idea : first define a bigger algebra
Take the vector space over $\mathbb{Q}$ with basis the formal symbols $I(\epsilon_1, \dots, \epsilon_k)$ for all convergent words. This becomes an algebra over $\mathbb{Q}$ where the basis elements multiply according to the shuffle rule.
This is the algebra $A_{1,0}$ of formal iterated integrals. It is graded by the weight.
The algebra of motivic multiple zeta values¶
Then consider the quotient algebra $A_\mathsf{MZV}$ by the ideal $K$ of $A_{1,0}$ generated by all relations that can be proved using the rules of calculus (using only algebraic change of variables in multiple integrals, plus linearity of integration).
This does make sense, even if this is very non-explicit and the ideal $K$ has no easy description. But the ideal $K$ is homogeneous for the weight, which is the dimension of the integration domain.
Francis Brown has proved the following fundamental result.
Theorem (Brown)
The algebra $A_\mathsf{MZV}$ has the generating series $1/(1-x^2-x^3)$. The set of elements $\zeta$ with arguments in $\{2,3\}$ is a basis.
Here one uses the same notation $\zeta(k_1,\dots,k_r)$ as in the real case.
The period map (digression)¶
Sending a formal iterated integral in $A_{1,0}$ to its numerical value (by actually computing the formal integral) defines a morphism from $A_{1,0}$ to $\mathbb{R}$.
This morphism factorises through the quotient $A_\mathsf{MZV}$.
The induced map from $A_\mathsf{MZV}$ to $\mathbb{R}$ is called the period map.
This is conjectured to be an injective map, hence an isomorphism to its image, which is the (non-motivic) algebra of multiple zeta values.
Special case of a very general period map, from the ring of abstract periods to $\mathbb{R}$ (Kontsevich-Zagier).
About the quotient map¶
So there is a quotient map (morphism of commutative algebras)
$$ K \longrightarrow A_{1,0} \stackrel{\Pi}{\longrightarrow} A_\mathsf{MZV}$$which is compatible with the weight. Here $K$ is the ideal of motivic relations.
Suppose that one can build a commutative sub-algebra $C$ of $A_{1,0}$ that is moreover a complementary subspace of the kernel ideal $K$.
Then the restriction of $\Pi$ to $C$ would be an isomorphism with $A_\mathsf{MZV}$.
Not easy to check the complementary condition, because $K$ is not explicit, but at least
AIM : build sub-algebras $C$ with the correct generating series.
Half shuffles and zinbiel algebras¶
Zinbiel algebras were introduced by Loday around 1995, as the Koszul dual notion to Leibniz algebras.
But considered and studied much before by Schützenberger in 1958 !
They are sometimes also given other names : dual Leibniz algebras, commutative dendriform algebras.
One could argue that the best name would be "half-shuffle algebras".
Definition : a zinbiel algebra over a field $k$ is a vector space $L$ over $k$ and a bilinear map $\prec \,: L\otimes_k L \to L$ such that, for all $x,y,z$ in $L$,
$$ (x \prec \color{red}{y}) \prec \color{green}{z} = x \prec (\color{red}{y} \prec \color{green}{z}) + x \prec (\color{green}{z} \prec \color{red}{y}). $$This may not look elegant and beautiful at first sight, but it is !
Claim / Exercise : if you define $x * y = x \prec y + y \prec x$ then $*$ is commutative and associative.
Fundamental example : free zinbiel algebras¶
Let us consider a finite set $S$, seen as an alphabet of letters.
Let $T(S)$ be the vector space spanned by all non-empty words in these letters.
One can endow $T(S)$ with the shuffle product, which is commutative and associative.
But more subtle : there is a zinbiel product on $T(S)$
$$ w \prec w' = \sum_{v} v$$where the sum is over all words $v$ in the shuffle of $w$ and $w'$ whose first letter come from $w$.
Slogan : one half of the shuffle product, according to the first letter
Free zinbiel algebras¶
Here is an example of this half-shuffle product of words:
$$(a,b) \prec (\color{red}{C,D}) = (a,b,\color{red}{C,D}) + (a,\color{red}{C},b,\color{red}{D}) + (a,\color{red}{C,D},b).$$The letter $a$ remains the first letter of every word in the product.
Easy claim : the symmetrized product $w * w' = w \prec w' + w' \prec w$ is the usual full shuffle product !
Theorem (Loday): T(S) is the free zinbiel algebra over $S$.
As fundamental as the polynomial rings (free commutative associative), in some sense.
The correct algebraic structure hidden behind the shuffle product !
Back to our business¶
Using the alphabet $S=\{0,1\}$, one gets the free zinbiel algebra $T(\{0,1\})$.
The algebra of formal iterated integrals $A_{1,0}$ is the commutative sub-algebra spanned by words starting with $1$ and ending with $0$ (recall the convergence conditions).
Easy claim : $A_{1,0}$ is a zinbiel sub-algebra of $T(\{0,1\})$. It is not free as a zinbiel algebra.
Note : $1/(1-x^2-x^3)$ is the generating series of the free zinbiel algebra $T(\{z_2,z_3\})$, when $z_2$ has weight $2$ and $z_3$ has weight $3$.
AIM : build a zinbiel algebra isomorphic to $T(\{z_2,z_3\})$, inside $A_{1,0}$
This will give a commutative graded sub-algebra of $A_{1,0}$ with the correct generating series.
Construction of free zinbiel sub-algebras¶
Let $u$ and $v$ be parameters, not both zero.
Define $z_2 = I(1,0)$ and $z_3 = u I(1,0,0)+v I(1,1,0)$ in $A_{1,0}$.
These are the generic elements of weight $2$ and $3$, most general possible choice.
Let $C_{u,v}$ be the zinbiel sub-algebra of $A_{1,0}$ generated by $z_2$ and $z_3$.
Theorem (FC) For all $(u,v)$, the zinbiel algebra $C_{u,v}$ is free on $z_2$ and $z_3$.
Hence $C_{u,v}$ has generating series $1/(1-x^2-x^3)$ as desired.
Proof : using bigrading by number of $0$ and number of $1$, leading terms for either grading and a little bit of combinatorics of half-shuffles.
The proof has to distinguish two cases : either $u\not=0$ or $v\not=0$.
Main conjecture¶
So now we have zinbiel hence commutative sub-algebras $C_{u,v}$ of $A_{1,0}$.
They only depends on $(u,v)$ up to common re-scaling $(\lambda u, \lambda v)$
Recall the projection map $\Pi$ to motivic multiple zeta values:
$$ K \longrightarrow A_{1,0} \stackrel{\Pi}{\longrightarrow} A_\mathsf{MZV}$$Then by restriction, one gets a short exact sequence
$$ K_{u,v} \longrightarrow C_{u,v} \stackrel{\Pi}{\longrightarrow} A_\mathsf{MZV}$$where $K_{u,v}$ is the intersection $K \cap C_{u,v}$.
Conjecture : for generic $(u,v)$, the kernel $K_{u,v}$ is zero and $\Pi$ becomes an isomorphism from $C_{u,v}$ to $A_\mathsf{MZV}$.
Here generic means : using $u,v$ as polynomial variables
Remarks¶
Conjecture (repeated) : for generic $(u,v)$, $\Pi$ is an isomorphism from $C_{u,v}$ to $A_\mathsf{MZV}$.
For some values of $(u,v)$, the map $\Pi$ is not an isomorphism :
Conjecture : the image of $C_{u,-u}$ is a sub-algebra of $A_\mathsf{MZV}$ with generating series $(1-x^3)/(1-x^2-x^3)$.
Something like a ring of multiple zeta values without $\zeta(3)$ ?
This resembles a little bit the generating series of $p$-adic multiple zeta values (Furusho), namely $(1-x^2)/(1-x^2-x^3)$. In this ring, no $\zeta(2)$.
Excluding that rather special case, one can assume $u+v=1$.
Non-singular values¶
Let us say that a value of $u$ is non-singular if $C_{u,1-u}$ is isomorphic via $\Pi$ to $A_\mathsf{MZV}$.
In this case, one can transfer properties from $C_{u,1-u}$ :
this algebra has a basis indexed by words in letters $2$ and $3$
the product in this basis is just the usual shuffle product of words
this algebra is bi-graded by the number of $2$ and the number of $3$
It would therefore be nice to find a non-singular $u$ : no one is known.
Some values are singular : roots of the determinants of change-of-basis matrices in small weights. Here is a picture of the first singular values in weight at most $12$
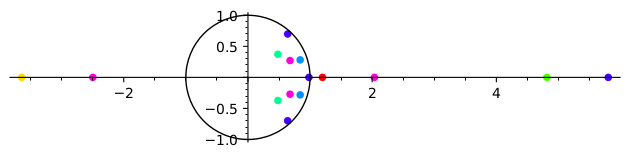
Some singular values are rational : $6/5$, $-51/14$, $4164/865$, etc.
Special cases¶
As possible good candidates for non-singular values of $u$,
one could look at $u=0$ and $u=1$.
This corresponds to $z_3 = I(1,1,0)$ and $z_3 = I(1,0,0)$.
In both cases, the image by $\Pi$ of every basis element of $C_{u,1-u}$ is an arborified multiple zeta value for some comb-shaped rooted tree.
Will not say much about those, also called branched zeta values. Replace the simplex (domain of integration in the iterated integrals) by a more complicated polytope, associated with a rooted tree seen as a partial order.
Essentially in bijection with zinbiel monomials in $A_{1,0}$, so that the product of two arborified multiple zeta values is a sum of two arborified multiple zeta values.
Studied by Clavier, Manchon, Ono and others.
What one would like¶
The algebra $A_\mathsf{MZV}$ has a very important structure, the motivic co-action, which plays an essential role.
- Is it possible to describe this co-action on the algebra $C_{u,1-u}$ in the basis of words in the letters $\{2,3\}$ ?
To use concretely $C_{u,1-u}$, one would also need to answer the following.
- How can one express the standard $\zeta(k_1,\dots,k_r)$ in the basis of $C_{u,1-u}$ ?
Both questions remain to be investigated, and may be difficult.
Récapitulons¶
Have build algebras $C_{u,v}$ and morphisms to $A_\mathsf{MZV}$ using zinbiel algebras.
Can hope that these morphisms are often iso, but may be hard to prove.
Special case $C_{u,-u}$ gives an interesting (?) sub-algebra of $A_\mathsf{MZV}$.
- The same idea and techniques should apply to alternating Multiple zeta values and more exotic algebras : multiple Landen values, multiple Watson values (Broadhurst).
🥨 Merci de votre attention 🥨Multizeta(1,2)**2
12*ζ(1,1,1,3) + 6*ζ(1,1,2,2) + 2*ζ(1,2,1,2)
M = Multizeta
(3*M(1,3)-M(2,2)).simplify_full()
0
Multizeta(1,2,3).n()
0.0323090289916699