Back to Hook Formulas Homepage
Hook Length Formulas for Partitions and Plane Trees
An explicit expansion formula for the
powers of the Euler Product in terms of partition hook lengths
By Guo-Niu Han
[download the paper: .ps -
.pdf, 35 pages, 2008/04/04]
Abstract.
We discover an explicit expansion formula for the powers s of
the Euler Product (or Dedekind η-function) in terms of
hook lengths of partitions, where the exponent s is any complex
number. Several classical formulas have been derived
for certain integers s
by Euler, Jacobi, Klein, Fricke, Atkin, Winquist, Dyson and Macdonald.
In particular, Macdonald obtained expansion formulas
for the integer exponents s for which there exists a semi-simple Lie algebra
of dimension s.
For the type Al(a) he has expressed
the (t2-1)-st power
of the Euler Product as a sum of weighted integer vectors of length t
for any integer t.
Kostant has considered the general case for any positive integer s
and obtained further properties.
The present paper proposes a new approach. We convert
the weighted vectors of length t used by Macdonald in his
identity for type Al(a) to
weighted partitions with
free parameter t, so that a new identity on the latter
combinatorial structures can be derived without any restrictions on t.
The surprise is that the
weighted partitions have a very simple form in terms of hook lengths
of partitions.
As applications of our formula, we find some
new identities about hook lengths, including the "marked hook
formula". We also improve a result due to Kostant.
The proof of the Main Theorem is based on Macdonald's identity for
Al(a)
and on the properties of
a bijection
between t-cores and integer vectors constructed by Garvan, Kim and Stanton.
The Main Theorem is the following hook length formula for partitions:
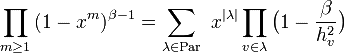
Summary
- Introduction. The Main Theorem. Selected results.
- Basic consequences and specializations.
- Equivalent forms.
- Corollaries.
- Specialization for β=0.
Generating function for partitions.
- Specialization for β=1.
- Specialization for β=∞.
Classical hook length formula and
the Robinson-Schensted-Knuth correspondence.
- Specialization for β=-1.
- Specialization for β=2.
Euler's pentagonal theorem.
Example for illustrating the Main Theorem.
- Specialization for β=25. Ramanujan τ-function.
Example for illustrating the Main Theorem.
- Specialization for β=4. Jacobi's triple product formula.
- Specialization for β=9.
- Proof of the Main Theorem.
- Fundamental properties of t-cores and V-codings.
- The bijection φV and an example.
- Proof of the first property.
- Proof of the second property.
- End of the proof of the Main Theorem.
- New formulas about hook lengths.
- Comparing the coefficients of β.
- Stanley-Elder-Bessenrodt-Bacher-Manivel Theorem.
- Comparing the coefficients of β2.
- Comparing the coefficients of &betanxn
and &betan-1xn.
The marked hook formula.
- Comparing the coefficients of
&betan-2xn
and of
&betan-3xn.
- Improvement of a result due to Kostant.
- The magic partition formula.
- Reversion of the Euler Product.
Back to Hook Formulas Homepage -
Last update: 2008/04/05