Main Page | Class Hierarchy | Class List | File List | Class Members | File Members | Related Pages

AffineAlgebra< K > Class Template Reference

#include <affinealgebras.H>

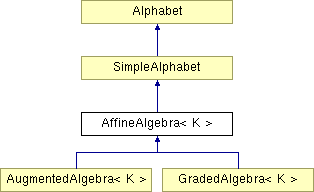
Inheritance diagram for AffineAlgebra< K >:

SimpleAlphabet Alphabet AugmentedAlgebra< K > GradedAlgebra< K > List of all members.

Detailed Description

template<class K>
class AffineAlgebra< K >

AffineAlgebra class.

An affine algebra is a finitely generated, commutative algebra over a ring K. So we store them as an alphabet (the generators) and an ideal (the relations). More precisely AffineAlgebra inherits from SimpleAlphabet and contains a variable Ideal<K>.

Most nontrivial operations require K to be a field. A few things are still possible when K is only a ring (naming the variables, adding relations, display the whole thing...)

Definition at line 25 of file affinealgebras.H.

Public Member Functions

 AffineAlgebra ()
 constructor /////////////////////////////////////////////////////////////////////////////
Polynomial< K > new_variable (const string &name)
 creates a new variable
Polynomial< K > one () const
 returns the constant polynomial, equal to 1, on the current alphabet
Tuple< Polynomial< K > > get_variables () const
 returns all the variables
void add_relation (const Polynomial< K > &rel)
 adds a generator in the relations ideal. Checks if it is 0, not if it is redundant.
long count_relations () const
 counts the relations
virtual void fix_alphabets ()
 fixes the alphabets of the relations, if needed
void find_grobner_basis ()
 replaces the relations by a minimal grobner basis
void reduce_grobner_basis ()
 self evident. Must already have computed a grobner basis.
Polynomial< K > reduced_form (const Polynomial< K > &f) const
 returns the division remainder of f with respect to the relations. More interesting if in grobner form!
bool is_finite_dimensional () const
 is the algebra finite dimensional over K ?
bool is_polynomial_variable (const Polynomial< K > &P) const
 returns true iff the polynomial is a single variable not showing up in the relations
virtual void swap_variables_order (long i, long j, list< Polynomial< K > > &polys)
 changes the order of two variables
virtual void swap_variables_order (long i, long j)
void tensor_with (const AffineAlgebra< K > &that)
 tensor product
bool top_variable_redundant (Polynomial< K > &result)
 checks if the top variable is in the subalgebra generated by the other variables
bool variable_redundant (long var, Polynomial< K > &result) const
 checks if a variable is in the subalgebra generated by the other variables
virtual void kill_top_variable (const Polynomial< K > &replacement, list< Polynomial< K > > &polys)
 replaces the top variable by a polynomial in the others
void kill_top_variable (const Polynomial< K > replacement)
void kill_variable (long var, const Polynomial< K > &replacement, list< Polynomial< K > > &polys)
 calls swap_variables_order then kill_top_variable. Order of the variables is modified.
void kill_variable (long var, const Polynomial< K > &replacement)
void cut_down_variables (list< Polynomial< K > > &polys)
 checks for all redundant variables.
void cut_down_variables ()
AbstractHomomorphism< K > find_redundancies ()
 find SOME redundancies in the variables and relations
AbstractHomomorphism< K > find_unitary_redundancies ()
 a variation on find_redundancies()

Public Attributes

bool verbose
 should display messages?
bool very_verbose
Ideal< K > relations
 self-explanatory

Friends

ostream & operator<< (ostream &os, const AffineAlgebra< K > &R)
ofstream & operator<< (ofstream &file, AffineAlgebra< K > &x)
void operator>> (ifstream &file, AffineAlgebra< K > &x)

Constructor & Destructor Documentation

template<class K>
AffineAlgebra< K >::AffineAlgebra (   )  [inline]
 

constructor /////////////////////////////////////////////////////////////////////////////

Member Function Documentation

template<class K>
void AffineAlgebra< K >::add_relation (  const Polynomial< K > &  rel  )  [inline]
 

adds a generator in the relations ideal. Checks if it is 0, not if it is redundant.

Reimplemented in GradedAlgebra< K >, and GradedAlgebra< F_2 >.

Definition at line 88 of file affinealgebras.H.

Referenced by AffineHomomorphism< F_2 >::compute_kernel(), AffineAlgebra< F_2 >::find_redundancies(), AffineAlgebra< F_2 >::find_unitary_redundancies(), AffineHomomorphism< F_2 >::is_essentially_contained_in(), AffineHomomorphism< F_2 >::is_essentially_surjective(), AffineHomomorphism< F_2 >::is_finite(), and AffineAlgebra< F_2 >::tensor_with().

template<class K>
long AffineAlgebra< K >::count_relations (   )  const [inline]
 

counts the relations

Definition at line 93 of file affinealgebras.H.

template<class K>
void AffineAlgebra< K >::cut_down_variables (  list< Polynomial< K > > &  polys  )  [inline]
 

checks for all redundant variables.

May be slow. Order of the variables wildly modified. Polynomials in polys are updated. Relies on variable_redundant().

Definition at line 411 of file affinealgebras.H.

template<class K>
void AffineAlgebra< K >::find_grobner_basis (   )  [inline]
 

replaces the relations by a minimal grobner basis

Definition at line 128 of file affinealgebras.H.

Referenced by AffineHomomorphism< F_2 >::compute_kernel(), HomFinder::define_polynomial_variables(), HomFinder::extend(), HomFinder::extend_all(), AffineAlgebra< F_2 >::find_redundancies(), AffineAlgebra< F_2 >::find_unitary_redundancies(), AffineHomomorphism< F_2 >::is_essentially_contained_in(), AffineHomomorphism< F_2 >::is_essentially_surjective(), AffineHomomorphism< F_2 >::is_finite(), HomFinder::test_steenrod(), and AffineAlgebra< F_2 >::top_variable_redundant().

template<class K>
AbstractHomomorphism<K> AffineAlgebra< K >::find_redundancies (   )  [inline]
 

find SOME redundancies in the variables and relations

This goes through the relations one by one and does the following:

  • Check if the relation has a "lonely" variable in the sense of Polynomial<K>::has_lonely_variable(). If so, the variable is killed and the relation discarded.
  • If not, it is checked using Grobner bases whether the relation is redundant with respect to the relations already checked. If so, it is discarded. If not, we move to the next relation to check.
In the end, the algebra has less variables, and less relations. The relations remaining come from the original ones: the grobner bases which are calculated in the process are not kept.

Note: The final presentation need not be minimal, unfortunately. However, there is an important case when a minimal presentation is produced: when the algebra is graded and the relations are (homogeneous and) stored with the degrees in nondecreasing order. Indeed, a relation of the form x=P(other variables) as above, if and when it is found, is the first one to involve the variable x at all. As a consequence, substituting x for something else does not modify the relations already added, and these do not present any redundancy, by construction.

Definition at line 478 of file affinealgebras.H.

template<class K>
AbstractHomomorphism<K> AffineAlgebra< K >::find_unitary_redundancies (   )  [inline]
 

a variation on find_redundancies()

Same as find_redundancies() except that it relies on Polynomial<K>::has_unitary_variable() rather than Polynomial<K>::has_lonely_variable(). Good when K is a ring but not a field.

Definition at line 564 of file affinealgebras.H.

template<class K>
virtual void AffineAlgebra< K >::fix_alphabets (   )  [inline, virtual]
 

fixes the alphabets of the relations, if needed

This makes sure that the polynomials in the relations have this as their alphabet. It is necessary, in particular, to call fix_alphabet after an assignment of the form A= B;

Todo:
make this a virtual method, and write an operator overload for =.

Reimplemented in UnstableAlgebra.

Definition at line 113 of file affinealgebras.H.

Referenced by HomFinder::define_polynomial_variables(), HomFinder::define_polynomial_variables_brutally(), HomFinder::extend(), HomFinder::extend_all(), UnstableAlgebra::fix_alphabets(), AffineHomomorphism< F_2 >::is_essentially_contained_in(), AffineHomomorphism< F_2 >::is_essentially_surjective(), AffineHomomorphism< F_2 >::is_finite(), MilnorAnalyzer::re_setup(), MilnorAnalyzer::setup_for_Sq1(), and AffineAlgebra< F_2 >::tensor_with().

template<class K>
Tuple< Polynomial<K> > AffineAlgebra< K >::get_variables (   )  const [inline]
 

returns all the variables

Definition at line 75 of file affinealgebras.H.

Referenced by GradedAlgebra< F_2 >::even_subalgebra(), HomFinder::extend(), HomFinder::extend_all(), MilnorAnalyzer::re_setup(), DerivationAnalyzer::setup(), MilnorAnalyzer::setup_for_Sq1(), and GradedAlgebra< F_2 >::top_degree().

template<class K>
bool AffineAlgebra< K >::is_finite_dimensional (   )  const [inline]
 

is the algebra finite dimensional over K ?

Requires LEX. A Grobner basis must have been computed.

Definition at line 150 of file affinealgebras.H.

Referenced by AffineHomomorphism< F_2 >::is_finite().

template<class K>
bool AffineAlgebra< K >::is_polynomial_variable (  const Polynomial< K > &  P  )  const [inline]
 

returns true iff the polynomial is a single variable not showing up in the relations

Definition at line 180 of file affinealgebras.H.

template<class K>
virtual void AffineAlgebra< K >::kill_top_variable (  const Polynomial< K > &  replacement,
list< Polynomial< K > > &  polys
)  [inline, virtual]
 

replaces the top variable by a polynomial in the others

This modifies the list polys so its members take the changes into account.

Reimplemented in AugmentedAlgebra< K >, GradedAlgebra< K >, RepresentationRing, UnstableAlgebra, AugmentedAlgebra< QQ >, and GradedAlgebra< F_2 >.

Definition at line 365 of file affinealgebras.H.

Referenced by GradedAlgebra< F_2 >::kill_top_variable(), AugmentedAlgebra< QQ >::kill_top_variable(), and AffineAlgebra< F_2 >::kill_variable().

template<class K>
void AffineAlgebra< K >::kill_variable (  long  var,
const Polynomial< K > &  replacement,
list< Polynomial< K > > &  polys
)  [inline]
 

calls swap_variables_order then kill_top_variable. Order of the variables is modified.

Definition at line 392 of file affinealgebras.H.

Referenced by AffineAlgebra< F_2 >::cut_down_variables(), AffineAlgebra< F_2 >::find_redundancies(), and AffineAlgebra< F_2 >::find_unitary_redundancies().

template<class K>
Polynomial<K> AffineAlgebra< K >::new_variable (  const string &  name  )  [inline]
 

creates a new variable

Returns:
a polynomial with only one monomial, namely the one variable just created, with coefficient one.

Reimplemented from SimpleAlphabet.

Definition at line 54 of file affinealgebras.H.

Referenced by AffineAlgebra< F_2 >::tensor_with().

template<class K>
Polynomial<K> AffineAlgebra< K >::one (   )  const [inline]
 

returns the constant polynomial, equal to 1, on the current alphabet

Definition at line 64 of file affinealgebras.H.

Referenced by HomFinder::branch(), Exponentiator< F_2 >::compute_exp_relations(), Exponentiator< F_2 >::compute_lambda_relation(), Exponentiator< F_2 >::compute_tensor_relation(), SW_Maker::create_regular_variables(), HomFinder::define_polynomial_variables(), HomFinder::define_polynomial_variables_brutally(), AffineHomomorphism< F_2 >::fill_zeroes(), GradedAlgebra< F_2 >::list_monomials(), HomFinder::polynomial_test(), MilnorAnalyzer::re_setup(), HomFinder::set_hom_from_matrix(), DerivationAnalyzer::setup(), MilnorAnalyzer::setup_for_Sq1(), HomFinder::sort(), SW_Maker::translate_homomorphism(), DerivationAnalyzer::write_gens(), and Exponentiator< F_2 >::write_lambda_factors().

template<class K>
void AffineAlgebra< K >::reduce_grobner_basis (   )  [inline]
 

self evident. Must already have computed a grobner basis.

Definition at line 133 of file affinealgebras.H.

Referenced by AffineHomomorphism< F_2 >::compute_kernel(), AffineAlgebra< F_2 >::find_redundancies(), AffineAlgebra< F_2 >::find_unitary_redundancies(), AffineHomomorphism< F_2 >::is_essentially_surjective(), and AffineHomomorphism< F_2 >::is_finite().

template<class K>
Polynomial<K> AffineAlgebra< K >::reduced_form (  const Polynomial< K > &  f  )  const [inline]
 

returns the division remainder of f with respect to the relations. More interesting if in grobner form!

Definition at line 137 of file affinealgebras.H.

Referenced by HomFinder::branch(), DerivationAnalyzer::constant_subalgebra(), HomFinder::extend(), HomFinder::extend_all(), AffineAlgebra< F_2 >::find_redundancies(), AffineAlgebra< F_2 >::find_unitary_redundancies(), AffineHomomorphism< F_2 >::is_essentially_contained_in(), AffineHomomorphism< F_2 >::is_essentially_surjective(), GradedAlgebra< F_2 >::list_monomials(), MilnorAnalyzer::re_setup(), MilnorAnalyzer::setup_for_Sq1(), HomFinder::test_steenrod(), and GradedAlgebra< F_2 >::top_degree().

template<class K>
virtual void AffineAlgebra< K >::swap_variables_order (  long  i,
long  j,
list< Polynomial< K > > &  polys
)  [inline, virtual]
 

changes the order of two variables

This corrects all the relations generators so they take the change of order into account. Likewise all polynomials created with this before should be modified.

Parameters:
 polys, a list of polynomials to update.

Reimplemented in AugmentedAlgebra< K >, GradedAlgebra< K >, RepresentationRing, UnstableAlgebra, AugmentedAlgebra< QQ >, and GradedAlgebra< F_2 >.

Definition at line 208 of file affinealgebras.H.

Referenced by AffineAlgebra< F_2 >::kill_variable(), GradedAlgebra< F_2 >::swap_variables_order(), and AugmentedAlgebra< QQ >::swap_variables_order().

template<class K>
void AffineAlgebra< K >::tensor_with (  const AffineAlgebra< K > &  that  )  [inline]
 

tensor product

Definition at line 238 of file affinealgebras.H.

Referenced by AffineHomomorphism< F_2 >::compute_kernel().

template<class K>
bool AffineAlgebra< K >::top_variable_redundant (  Polynomial< K > &  result  )  [inline]
 

checks if the top variable is in the subalgebra generated by the other variables

returns true if so. Also, in this case, result contains a replacement for the top variable in terms of the others (otherwise the value of result is bogus). Requires LEX.

Definition at line 276 of file affinealgebras.H.

template<class K>
bool AffineAlgebra< K >::variable_redundant (  long  var,
Polynomial< K > &  result
)  const [inline]
 

checks if a variable is in the subalgebra generated by the other variables

Similar to kill_top_variable(), but better. Can proceed with any variable instead of just the top one. Uses DEGLEX with an elimination order, which is usually faster than LEX. However it uses an order override, which is sometimes inefficient, so kill_top_variable() may sometimes be just as good.

Returns:
true iff the variable is redundant. In this case, result contains a polynomial P expressing the variable in terms of the other.

Definition at line 321 of file affinealgebras.H.

Referenced by AffineAlgebra< F_2 >::cut_down_variables().

Member Data Documentation

template<class K>
Ideal<K> AffineAlgebra< K >::relations
 

self-explanatory

Definition at line 36 of file affinealgebras.H.

Referenced by SW_Maker::add_complex_relations(), Exponentiator< F_2 >::add_relations(), Exponentiator< F_2 >::clean_up_equations(), AffineHomomorphism< F_2 >::compute_kernel(), DerivationAnalyzer::constant_subalgebra(), HomFinder::init(), MilnorAnalyzer::setup_for_Sq1(), and AffineAlgebra< F_2 >::tensor_with().

template<class K>
bool AffineAlgebra< K >::verbose
 

should display messages?

Definition at line 32 of file affinealgebras.H.

Referenced by Exponentiator< F_2 >::compute_exp_relations().

The documentation for this class was generated from the following file:
Generated on Wed Jun 18 17:22:43 2008 for Pierre Guillot by  doxygen 1.3.9.1