An exponentiator takes a representation ring and creates an associated graded algebra, the "exp" ring. In the comments, we say exp-classes for either Chern or Stiefel-Whitney classes.
|
Public Member Functions |
| virtual void | create_regular_variables (string prefix) |
| | creates the variables in *target
|
| void | create_extra_variables (string prefix) |
| | creates a bunch of temporary variables
|
| void | kill_extra_variables () |
| | as it says, really.
|
| void | clean_up_equations () |
| | cleaned up equations
|
| Polynomial< K > | compute_tensor_relation (long max_dim1, long max_dim2) |
| | computes the universal polynomial for the exp classes of a tensor product
|
| void | write_lambda_factors (list< Polynomial< K > > &result, long ext, long first, long last) |
| | internal use only -- used by compute_lambda_relation()
|
| Polynomial< K > | compute_lambda_relation (long ext, long dim) |
| | computes the universal polynomial for the exp classes of an external power
|
| void | exp_classes_after_tensoring (const Polynomial< K > &exp, long dim, const PowProd &pow, Polynomial< K > &result) |
| | recursively compute the exp classes of a tensor product
|
| Polynomial< K > | exp_classes_of_ext_power (long thevar, long ext) |
| | compute the exp classes of an exterior power of a representation
|
| void | compute_exp_relations () |
| | translate the equations in *source into equations in *target
|
|
void | split_and_sort () |
| void | add_relations () |
| | adds the relations to *target from exp_relations
|
| void | start (RepresentationRing *thesource, GradedAlgebra< K > *thetarget, string prefix, long thefactor) |
| | gets the computation going
|
Public Attributes |
| RepresentationRing * | source |
| | the representation ring
|
| GradedAlgebra< K > * | target |
| | the outcome - a graded algebra
|
| long | last_actual_variable |
| | remembers the number of "regular" variables.
|
| long | max_dim |
| | largest dimension of a rep among the variables in *source
|
| long | max_dim_rel |
| | largest dimension of a rep among the relations in *source
|
| Table< Polynomial< K > > | var |
| | the "regular" variables created in *target, as polynomials
|
| Tuple< Polynomial< K > > | a |
| | the "extra" variables, as polynomials
|
| Tuple< Polynomial< K > > | b |
| | the "extra" variables, as polynomials
|
| Tuple< Polynomial< K > > | s |
| | the "extra" variables, as polynomials
|
| Tuple< Polynomial< K > > | sp |
| | the "extra" variables, as polynomials
|
list< pair< Polynomial< QQ >,
Polynomial< QQ > > > | equations |
| | cleaned up equations
|
| list< Polynomial< K > > | total_relations |
| | all resulting total relations between exp classes
|
| list< Polynomial< K > > | exp_relations |
| | same as total_relations, only homogeneous and sorted by degree
|
| long | factor |
| | typically 2 for Chern classes, 1 for SW
|
map< pair< long, long >, Polynomial<
K > > | univ_computed |
| | universal polynomials for tensor products
|
map< pair< long, long >, Polynomial<
K > > | lambda_univ_computed |
| | universal polynomial for lambda operations
|
|
|
gets the computation going
This is the first thing to read in the comments. This method calls all the others in a precise order. It is possible to use some of the methods independantly, but mostly they should be use only in this order (follow the links to find out what each method does):
-
First there is a call to create_regular_variables(). Note that this sets up max_dim, and populates var.
- See also:
- max_dim, var
-
Then clean_up_equations() is invoked. This is the time when max_dim_rel is computed.
- See also:
- max_dim_rel
-
Next we call create_extra_variables(), which needs to know max_dim_rel and max_dim. It populates a, b, s and sp.
- See also:
- a, b, s, sp (follow this link for a summary of all the variables created.)
-
Then comes compute_exp_relations(), doing the actual work. This fills total_relations (see note 2 below).
-
split_and_sort() is here next, to split the relations into homogeneous parts and add them to exp_relations in nondecreasing order of degree.
-
We kill the temporary variables which were needed before, using kill_extra_variables().
-
Finally, add_relations() takes the relations in exp_relations, adds them to *target and releases some memory..
Note 1: After all this, you may want to run target->find_redundancies() in order to simplify the presentation.
Note 2: It is not expected that total_relations is empty before we start. Indeed, the class SW_Maker, which inherits from Exponentiator<F_2>, exploits this by adding some total relations before things get started (in turn, these are relations coming from another Exponentiator<F_2>, namely Chern_Maker).
Definition at line 841 of file exp_classes.H.
Referenced by SW_Maker::start(). |
|
|
the "extra" variables, as polynomials
Here's a summary of all the variables created:
-
The variables numbered 1 to last_actual_variable are the exp classes of the variables in *source. They are stored as var[i,j].
- See also:
- var.
-
The variables last_actual_variable + 1 to last_actual_variable + max_dim are formal "roots" needed for the splitting principle, and they are stored as polynomials under a[1], a[2], ..., a[max_dim].
-
Similarly, the next variables are roots, stored as b[1], b[2], ..., b[max_dim_rel].
-
The next variables (max_dim of them) are used as generic exp classes, stored as s[1], ..., s[max_dim], and we think of s[i] as the i-th symmetric function in the a[j]'s.
-
Likewise for the final set of variables, stored as sp[1], ..., sp[max_dim_rel], (sp for s prime), thought of as symmetric functions in the b[j]'s.
Definition at line 88 of file exp_classes.H. |
|
|
the "extra" variables, as polynomials
Here's a summary of all the variables created:
-
The variables numbered 1 to last_actual_variable are the exp classes of the variables in *source. They are stored as var[i,j].
- See also:
- var.
-
The variables last_actual_variable + 1 to last_actual_variable + max_dim are formal "roots" needed for the splitting principle, and they are stored as polynomials under a[1], a[2], ..., a[max_dim].
-
Similarly, the next variables are roots, stored as b[1], b[2], ..., b[max_dim_rel].
-
The next variables (max_dim of them) are used as generic exp classes, stored as s[1], ..., s[max_dim], and we think of s[i] as the i-th symmetric function in the a[j]'s.
-
Likewise for the final set of variables, stored as sp[1], ..., sp[max_dim_rel], (sp for s prime), thought of as symmetric functions in the b[j]'s.
Definition at line 88 of file exp_classes.H. |
|
|
the "extra" variables, as polynomials
Here's a summary of all the variables created:
-
The variables numbered 1 to last_actual_variable are the exp classes of the variables in *source. They are stored as var[i,j].
- See also:
- var.
-
The variables last_actual_variable + 1 to last_actual_variable + max_dim are formal "roots" needed for the splitting principle, and they are stored as polynomials under a[1], a[2], ..., a[max_dim].
-
Similarly, the next variables are roots, stored as b[1], b[2], ..., b[max_dim_rel].
-
The next variables (max_dim of them) are used as generic exp classes, stored as s[1], ..., s[max_dim], and we think of s[i] as the i-th symmetric function in the a[j]'s.
-
Likewise for the final set of variables, stored as sp[1], ..., sp[max_dim_rel], (sp for s prime), thought of as symmetric functions in the b[j]'s.
Definition at line 88 of file exp_classes.H. |
|
|
the "extra" variables, as polynomials
Here's a summary of all the variables created:
-
The variables numbered 1 to last_actual_variable are the exp classes of the variables in *source. They are stored as var[i,j].
- See also:
- var.
-
The variables last_actual_variable + 1 to last_actual_variable + max_dim are formal "roots" needed for the splitting principle, and they are stored as polynomials under a[1], a[2], ..., a[max_dim].
-
Similarly, the next variables are roots, stored as b[1], b[2], ..., b[max_dim_rel].
-
The next variables (max_dim of them) are used as generic exp classes, stored as s[1], ..., s[max_dim], and we think of s[i] as the i-th symmetric function in the a[j]'s.
-
Likewise for the final set of variables, stored as sp[1], ..., sp[max_dim_rel], (sp for s prime), thought of as symmetric functions in the b[j]'s.
Definition at line 88 of file exp_classes.H. |
![\[P= \prod_{1\le i \le maxdim1,\\ 1\le j \le maxdim2} (1 + a_i + b_j) \]](form_4.png)
![\[ P=Q(\sigma_1, \sigma_2, \ldots, \sigma'_1, \sigma'_2, \ldots) \]](form_2.png)
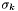 is the k-th symmetric function in the a_i's (resp ... obvious). Then, Q(w_i, w'_j) is the total exp class of the tensor product of the two representations with exp classes w_i and w'_j respectively.
is the k-th symmetric function in the a_i's (resp ... obvious). Then, Q(w_i, w'_j) is the total exp class of the tensor product of the two representations with exp classes w_i and w'_j respectively. 1.3.9.1
1.3.9.1