Lois de conservations scalaires

Section 1.1 Lois de conservations scalaires

Dans ce chapitre, on se concentrera sur le cas des lois de conservation scalaires et plus particulièrement sur l'équation d'advection linéaire et l'équation de Burgers (très proche du modèle LWR de trafic routier).

Subsection 1.1.1 Loi de conservations

Définition 1.1.1.

Une loi de conservation scalaire est une EDP qui satisfait le problème de Cauchy suivant:

\begin{equation} \begin{cases} \partial_t \rho+ \partial_x f(\rho)=0 \\ \rho(t=0,x)=\rho_0(x) \end{cases}\tag{1.1.1} \end{equation}

avec \(\rho_0(x)\in C^1(\mathbb{R})\text{.}\)

On note \(a(\rho)=f^{'}(\rho)\) la Jacobienne du flux.

On parle de loi de conservation car si n'y a pas d'information qui rentre dans le domaine ou lorsque le domaine est infini et la condition initiale a support compact, alors par le théorème de Green on obtient que l'intégrale \(\int_{\Omega}\rho dx\) est conservée en temps.

On va regarder les problèmes d'existence et d'unicité en essayant de déterminer à la main une solution. On va aussi introduire une notion appelée courbes caractéristiques.

Définition 1.1.2. Courbes caractéristiques.

Les courbes caractéristiques sont des courbes paramétrées \(X(t,X_0)\) qui satisfait l'équation:

\begin{equation} \begin{cases} \frac{d X(t;X_0)}{dt}=a(\rho(t,X(t;X_0))) \\ X(t=0,X_0)=X_0\end{cases}\tag{1.1.2} \end{equation}

On va voir que ces courbes caractéristiques vont nous permettre de caractériser des solutions. On se place d'abord dans le cas linéaire \(f(\rho)=a\rho\text{.}\) Dans ce cas l'équation caractéristique devient:

\begin{equation} \frac{d X(t;X_0)}{dt}=a\tag{1.1.3} \end{equation}

et la solution est naturellement donnée par \(X(t,x)=x+at\text{.}\) Maintenant on va voir comme ces courbes caractéristiques permettent de définir les solutions de notre équation.

Théorème 1.1.3.

Soit \(\rho_0(x)\in C^{1}(\mathbb{R})\text{.}\) Alors il existe une unique solution \(\rho(t,x)\in C^1{\mathbb{R}^+\times \mathbb{R}}\) de l'équation (1.1.1) avec \(f(\rho)=a\rho\text{.}\) La solution est obtenue par

\begin{equation*} \rho(t,X(t;x))=\rho_0(t,X(0;x)) \end{equation*}

avec \(X(t;x)\) solution de (1.1.3) ce qui équivaut à:

\begin{equation*} \rho(t,x)=\rho_0(x-at) \end{equation*}

Preuve.

Le résultat revient a dire que la courbe caractéristique est constante en temps le long des solutions \(u(t,x)\text{.}\) En utilisant la formule de la différentielle et la régularité de la solution, on obtient:

\begin{equation*} \frac{d \rho(t,X(t;x))}{dt}=\partial_t \rho + X^{'}(t,x)\partial_x \rho \end{equation*}

Par définition de la courbe caractéristique on a \(X^{'}(t,x)=a\text{.}\) Donc

\begin{equation*} \frac{d \rho(t,X(t;x))}{dt}=\partial_t \rho + a\partial_x \rho=0 \end{equation*}

ce qui clot la démonstration.

On voit que les courbes caractéristiques nous permettent de déterminer la solution qui est une translation de la condition initiale. Maintenant l'enjeu va être d'étendre ce résultat dans le cadre nonlinéaire. Ici contrairement au cas linéaire la caractéristique dépend de \(u\) dont à priori on se connaît pas la régularité. On va maintenant introduire deux résultats qui montrent la difficulté du problème.

Proposition 1.1.4.

On suppose \(\rho_0(x)\) suffisamment régulière. Pour des temps suffisamment petit il existe une unique solution de (1.1.1). La solution est obtenue par

\begin{equation*} \rho(t,X(t;x))=\rho_0(t,X(0;x)) \end{equation*}

avec \(X(t;x)\) solution de (1.1.2) ce qui équivaut à:

\begin{equation*} \rho(t,x+tf^{'}(\rho_0(x)))=\rho_0(x) \end{equation*}

Preuve.

\begin{equation*} \frac{d \rho(t,X(t;x))}{dt}=\partial_t \rho + X^{'}(t,x)\partial_x \rho \end{equation*}

Par définition de la courbe caractéristique on a \(X^{'}(t,x)=a(\rho(t,X(t;x)))\text{.}\) Donc

\begin{equation*} \frac{d \rho(t,X(t;x))}{dt}=\partial_t \rho + (a(\rho(t,X(t;x))))\partial_x \rho \end{equation*}

Puisque la solution est régulière on a

\begin{equation*} \partial_t \rho + a(\rho)\partial_x \rho =\partial_t \rho + f^{'}(\rho)\partial_x \rho =\partial_t \rho +\partial_x f(\rho) =0 \end{equation*}

ce qui clot la démonstration.

Comme précédemment on voit que la solution \(\rho \) est préservée le long des caractéristiques. Cependant cela est possible que si la solution reste régulière. On voit que contrairement au cas linéaire ou les caractéristiques restent parallèles dans le cas nonlinéaire elles peuvent a priori se croiser ce qui génère une solution multi-valuée et donc discontinue.

Proposition 1.1.5.

Si il existe deux reels \(x_0 \lt x_1\) tel que \(f^{'}(\rho_0(x_0))\gt f^{'}(\rho_0(x_1))\) alors la solution régulière de la proposition précédente n'existe plus globalement en temps. Le temps maximal d'existence est

\begin{equation*} T_{inf}=\operatorname{inf}_{x_0 \lt x_1}\frac{x_1-x_0}{(f^{'}(\rho_0(x_0)) \gt f^{'}(\rho_0(x_1)))^{+}} \end{equation*}

Preuve.

Admis

Remarque 1.1.6.

Dans le cas du transport linéaire constant \(f(\rho)=a\rho\) la condition de la proposition précédente n'est pas satisfaite et dans on a existence globale en temps de la solution régulière précédente si la donnée initiale est elle-même régulière.

Le résultat de la Proposition 1.1.5 montre qu’au bout d’un certain temps (fini) les EDP hyperboliques nonlinéaires font apparaître des discontinuités en temps. Il n'existe donc pas de solution forte (au sens \(C^p\)) que sur temps fini potentiellement petit. Pour pouvoir traiter ce problème, il est donc naturel d'utiliser une notion de solution faible pour nos EDP.

Définition 1.1.7. Solution faible.

Soit \(\rho_0\in L^{\infty}(\mathbb{R})\) on appelle solution faible de (1.1.1) la fonction \(\rho\in L^{\infty}(\mathbb{R} \times \mathbb{R}^{+})\) si et seulement si elle satisfait

\begin{equation} \int_{\mathbb{R}}\int_{\mathbb{R}^{+}}(\rho\partial_t \phi + f(\rho)\partial_x \phi)dxdt+\int_{\mathbb{R}}\rho_0(x)\phi(0,x)dx=0\tag{1.1.4} \end{equation}

pour toute fonction \(\phi \in C_0^{\infty}(\mathbb{R} \times \mathbb{R}^{+})\text{.}\)

On ne le démontrera pas, mais évidemment si on a une solution forte elle est aussi solution faible. On voit en faîte qu'il s'agit de l'équation hyperbolique intégrée contre des fonctions régulières. Cette notion va nous permettre donc de considérer des solutions discontinues comme on va le voir par la suite.

Proposition 1.1.8. Caractérisation des discontinuités.

Soit une courbe \(\Gamma=\left\{(x,t) \in \mathbb{R} \times \mathbb{R}^{+} / x=\sigma(t)\right\}\) avec \(\sigma(t)\in C^1(\mathbb{R})\) coupant un ouvert \(\Omega\) en deux parties \(\Omega_{-}=\left\{ (t,x)\in \Omega, x \lt \Gamma(t) \right\}\) et \(\Omega_{+}=\left\{ (t,x)\in \Omega, x \gt \Gamma(t) \right\}\text{.}\) On considère \(\rho\in C^1(\Omega)_{-} \cap C^1(\Omega)_{+}\) alors \(\rho\) est solution faible (1.1.1) si et seulement si

\begin{equation} -\sigma^{'}(t)(\rho^{+}-\rho^{-})=f(\rho^{+})-f(\rho^{-})\tag{1.1.5} \end{equation}

avec \(\rho^{\pm}=\rho(t,\sigma^{\pm})\) qui sont les limites à gauche et à droite de \(\Gamma(t)\) et \(\rho\) une solution forte de (1.1.1) sur \(\Omega/\Gamma\text{.}\) On appelle (1.1.5) les relations de Rankine Hugoniot.

Preuve.

On commence par partie d'une solution faible (1.1.4) sans la condition en temps que l'on rappelle

\begin{equation} A= \int_{\mathbb{R}}\int_{\mathbb{R}^{+}}(\rho\partial_t \phi + f(\rho)\partial_x \phi)dxdt=0\tag{1.1.6} \end{equation}

On coupe en deux

\begin{equation} A=\int_{\Omega_{-}}(\rho\partial_t \phi + f(\rho)\partial_x \phi)dxdt +\int_{\Omega^{+}}(\rho\partial_t \phi + f(\rho)\partial_x \phi)dxdt=0\tag{1.1.7} \end{equation}

On le réécrit légèrement pour simplifier la suite:

\begin{equation} A=\int_{\Omega_{-}}\left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \nabla_{t,x}\phi dxdt +\int_{\Omega_{+}}\left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \nabla_{t,x}\phi dxdt=0\tag{1.1.8} \end{equation}

On pratique une intégration par partie sur chaque bout pour obtenir \(A=A_{+} + A_{-}=0\text{:}\)

\begin{equation} A_{\pm}=\int_{\Gamma}\left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \bs{n}_{\pm}\phi dxdt - \int_{\Omega^{\pm}}(\partial_t\rho \phi + \partial_x f(\rho)\phi)dxdt= 0\tag{1.1.9} \end{equation}

Les deux intégrales sur \(\Omega_{\pm}\) sont nulles car on a considéré que \(\rho\) est solution forte sur chaque domaine \(\Omega_{\pm}\text{.}\) On a donc

\begin{equation} \int_{\Gamma}\left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \bs{n}_{+}\phi dxdt + \int_{\Gamma}\left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \bs{n}_{-}\phi dxdt =0\tag{1.1.10} \end{equation}

Puisque \(\phi\) est arbitraire on obtient une condition nécessaire et suffisante pour avoir l'égalité (1.1.10) donné par

\begin{equation} \left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \bs{n}_{+} + \left(\begin{array}{c} \rho \\ f(\rho)\end{array} \right)\cdot \bs{n}_{-} =0, \quad (x,t)\in \Gamma\tag{1.1.11} \end{equation}

On remarque que les normales vérifient

\begin{equation*} \bs{n}_{-}=-\bs{n}_{+}=K\begin{pmatrix} -\sigma^{'}(t) \\ 1\end{pmatrix} \end{equation*}

En appliquant cette forme à l'équation (1.1.11) on obtient le résultat (1.1.5).

On a donc introduit la notion de solution faible pour des équations hyperboliques. Cette notion nous permet de tenir compte des solutions discontinues qu'on a vues émerger avec l'étude des caractéristiques. Cependant cette notion n'est pas suffisante pour bien caractériser le problème. En effet si on considère l'équation de Burgers:

\begin{equation*} \partial_t \rho + \partial_x\left(\frac{\rho^2}{2}\right)=0 \end{equation*}

avec pour solution initiale

\begin{equation} \rho_0(x)=\begin{cases} \rho_l, \quad x\lt 0 \\ \rho_r, \quad x \gt 0 \end{cases}\tag{1.1.12} \end{equation}

alors la fonction

\begin{equation} \rho(t,x)=\begin{cases} \rho_l, \quad x\lt -s_1 t \\ -a, \quad -s_1 t \lt x \lt 0 \\ a, \quad 0 \lt x \lt s_2 t \\ \rho_r, \quad x \gt s_2 t \end{cases}\tag{1.1.13} \end{equation}

avec \(s_1=\frac{\rho_l-a}{2}\text{,}\) \(s_2=\frac{\rho_r+a}{2}\) et \(a \ge max(\rho_l,-\rho_r)\) est solution \(\forall a >0\text{.}\) On a donc pas unicité de la solution faible.

Maintenant on va chercher a établir une notion qui nous permet de récupérer l'unicité des solutions. Pour cela on va admettre un résultat.

Théorème 1.1.9. Admis.

Soit l'équation

\begin{equation} \begin{cases} \partial_t \rho_{\epsilon}+ \partial_x f(\rho_{\epsilon})=\epsilon \partial_{xx}\rho_{\epsilon} \\ \rho_{\epsilon}(t=0,x)=\rho_{0,\epsilon}(x) \end{cases}\tag{1.1.14} \end{equation}

avec \(\rho_{0,\epsilon}(x)\in C^2(\mathbb{R})\text{.}\) Alors il existe une unique solution régulière de classe au moins \(C^2(\mathbb{R}\times \mathbb{R}_{+})\text{.}\)

L'idée est de déterminer une notion d'unicité à partir des solutions visqueuses précédentes. L'introduction de cette notion est assez logique. En effet il est assez naturel en physique de considérer des systèmes avc un peu de viscosité et donc de voir les problèmes hyperboliques comme des limites de ces modèles faiblement visqueux.

solution entropique

Définition 1.1.10.

Soit l'équation (1.1.1). Soit fonction \(\eta \in C^2(\mathbb{R})\) convexe. Soit la fonction \(\zeta: \mathbb{R} \rightarrow \mathbb{R}\) définie par

\begin{equation*} \zeta^{'}(\rho)=\eta^{'}(\rho)f^{'}(\rho), \quad \zeta(\rho)=\int \eta^{'}(\rho)f^{'}(\rho) \end{equation*}

Ce couple de fonctions \((\eta,\zeta)\) est appelé entropie-flux entropique. Si pour toute solution régulière de (1.1.1) on a

\begin{equation*} \partial_t \eta(\rho) + \partial_x \zeta(\rho)=0 \end{equation*}

Exemple 1.1.11.

On considère l'équation de Burgers avec le flux \(\frac{\rho^2}{2}\text{.}\) Quelles fonctions peuvent former un couple entropie-flux entropique pour cette équation.

Answer.

Les fonctions du type

\begin{equation*} \eta_p(\rho)=\frac{u^{2p}}{2p}+\alpha\frac{\rho^2}{2} \end{equation*}

sont des entropies pour Burgers avec comme flux entropiques associés:

\begin{equation*} \zeta_p(\rho)=\frac{u^{2p+1}}{2p+1}+\alpha\frac{\rho^3}{3} \end{equation*}

Maintenant ces notions introduites, on va pouvoir construire un nouveau type de solution faible à partir des solutions visqueuses.

Définition 1.1.12. Solution faible entropique.

Soit \(\rho_0\in L^{\infty}(\mathbb{R})\) on appelle solution faible entropique de (1.1.1) la fonction \(\rho\in L^{\infty}(\mathbb{R} \times \mathbb{R}^{+})\) si et seulement si elle satisfait

\begin{equation} \int_{\mathbb{R}}\int_{\mathbb{R}^{+}}(\eta(\rho)\partial_t \phi + \zeta(\rho)\partial_x \phi)dxdt+ \int_{\mathbb{R}}\eta(\rho_0(x))\phi(0,x)dx \ge 0\tag{1.1.15} \end{equation}

pour toute fonction \(\phi \in C_0^{\infty}(\mathbb{R} \times \mathbb{R}^{+})\text{.}\) Il s'agit de l'inégalité suivante

\begin{equation*} \partial_t \eta(\rho) + \partial_x \zeta(\rho) \leq 0 \end{equation*}

au sens des distributions.

Théorème 1.1.13.

Soit \(\rho_{\epsilon}\) une solution (1.1.14) tel que \(\Norm \rho_{\epsilon}\Norm_{L_{loc}^1(\mathbb{R}^{+}\times\mathbb{R} )} \leq C\text{.}\) Si la limite \(\rho\) de \(\rho_{\epsilon}\) satisait

\begin{equation*} \operatorname{lim}_{\epsilon \rightarrow 0^{+}}\Norm \rho_0 -\rho_{0,\epsilon}\Norm_{L_{loc}^1(\mathbb{R} )}=0 \end{equation*}

\begin{equation*} \operatorname{lim}_{\epsilon \rightarrow 0^{+}}\Norm \rho -\rho_{\epsilon}\Norm_{L_{loc}^1(\mathbb{R}^{+}\times\mathbb{R} )}=0 \end{equation*}

alors

solution faible au sens de (1.1.4),
solution faible entropique au sens de (1.1.15) pour \(\phi\in C_0^{\infty}(\Omega)\) et \(\phi \ge 0\)

Preuve.

On commence avec (1.1.14). On multiple par \(\eta^{'}(\rho)\) ce qui donne

\begin{equation*} \partial_t \eta(\rho_{\epsilon})+\eta^{'}(\rho_{\epsilon})f^{'}(\rho_{\epsilon})\partial_x \rho_{\epsilon}= \epsilon \eta^{'}(\rho_{\epsilon})\partial_{xx}\rho_{\epsilon} \end{equation*}

Cela se réécrit par définition de entropie et du flux entropique

\begin{equation*} \partial_t \eta(\rho_{\epsilon})+\partial_x\zeta(\rho_{\epsilon})= \epsilon \partial_{xx}\eta(\rho_{\epsilon})-\epsilon\eta^{''}(\rho_{\epsilon}) \left(\partial_{x}\rho_{\epsilon}\right)^2 \leq \epsilon\partial_{xx}\eta(\rho_{\epsilon}) \end{equation*}

À partir de la on multiplie par une fonction test et on intègre pour obtenir

\begin{equation*} \int_{\mathbb{R}}\int_{\mathbb{R}^{+}} \partial_t\eta(\rho_{\epsilon})\phi dt dx \int_{\mathbb{R}}\int_{\mathbb{R}^{+}}\partial_x\zeta(\rho_{\epsilon})\phi dt dx \le \epsilon\int_{\mathbb{R}}\int_{\mathbb{R}^{+}} \partial_{xx}\eta(\rho_{\epsilon})\phi dt dx \end{equation*}

On intègre par partie pour avoir

\begin{equation*} -\int_{\mathbb{R}}\int_{\mathbb{R}^{+}} \left(\eta(\rho_{\epsilon})\partial_t\phi+ \zeta(\rho_{\epsilon})\partial_x\phi\right) dt dx - \int_{\mathbb{R}}\eta(\rho_0(x))\phi(0,x)dx \le \epsilon\int_{\mathbb{R}}\int_{\mathbb{R}^{+}} \partial_{xx}\eta(\rho_{\epsilon})\phi dt dx \end{equation*}

On va maintenant regarder la convergence des intégrales à gauche. On s'occupe de la première. Les autres pourront être obtenues avec les mêmes arguments. On regarde \(A\)

\begin{equation*} A=\int_{\mathbb{R}}\int_{\mathbb{R}^{+}} \left(\eta(\rho_{\epsilon})\partial_t\phi - \eta(\rho)\partial_t\phi\right) dx dt \end{equation*}

On définit \(S(\phi)=\left\{(t,x)\in \mathbb{R}^+\times \mathbb{R}: \phi(t,x)>0 \right\}\text{.}\) On utilise le fait que la fonction test est infiniment dérivable et donc bornée. On a donc

\begin{equation*} \mid A\mid \le \left(\operatorname{max}\mid \partial_t \phi\mid\right) \int_{S(\phi)}\left(\eta(\rho_{\epsilon}) - \eta(\rho)\right) dx dt \end{equation*}

Ensuite on utilise que \(\eta\) est convexe et la norme infinie de la solution est bornée par \(C\text{.}\) Donc

\begin{equation*} \mid A\mid \le \left(\operatorname{max}\mid \partial_t \phi\mid \operatorname{max}_{\mid v\mid \le C}\mid \eta^{'}(v)\mid\right) \int_{S(\phi)} \left(\rho_{\epsilon} - \rho\right) dx dt \end{equation*}

On a donc convergence de l'intégrale car la fonction \(\rho_{\epsilon}\) converge vers \(\rho\) dans \(L_{loc}^1\) par hypothèse. On obtient la convergence des autres intégrales de même façon. Le terme de droite peut être borné et donc tend vers zéro quand \(\epsilon\) tend vers zéro. Cela permet de conclure.

Proposition 1.1.14. Caractérisation des discontinuités entropique.

\begin{equation} -\sigma^{'}(t)(\rho^{+}-\rho^{-})+f(\rho^{+})-f(\rho^{-})=0\tag{1.1.16} \end{equation}

\begin{equation} -\sigma^{'}(t)(\eta(\rho^{+})-\eta(\rho^{-}))+\zeta(\rho^{+})-\zeta(\rho^{-})\leq 0\tag{1.1.17} \end{equation}

pour tout couple \((\eta,\zeta)\) avec \(\rho^{\pm}=\rho(t,\sigma^{\pm})\) qui sont les limites à gauche et à droite de \(\Gamma(t)\) et \(\rho\) une solution forte de (1.1.1) sur \(\Omega/\Gamma\text{.}\)

Preuve.

A faire en TD.

Maintenant on va essayer d'avoir une caractérisation plus exploitable des discontinuités entropiques que les caractérisations (1.1.16) - (1.1.17). On le fera uniquement dans le cas d'un flux convexe, mais des résultats existent dans le cas général.

Proposition 1.1.15.

On se donne un flux \(f\in C^2(\mathbb{R})\) strictement convexe. Soit une discontinuité \((\sigma,\rho_l,\rho_r)\) satisfaisant (1.1.16) - (1.1.17) alors on a nécessairement

\begin{equation*} \rho_{-} \ge \rho_{+} \end{equation*}

Preuve.

On considère \(\rho_l \neq \rho_r\text{.}\) On va commencer par définir deux fonctions

\begin{equation} g(\rho)= f(\rho)-f(\rho_r)-\sigma(\rho-\rho_r)\tag{1.1.18} \end{equation}

\begin{equation} h(\rho)= \zeta(\rho)-\sigma\eta(\rho)\tag{1.1.19} \end{equation}

La condition de Ranke-Hugoniot (1.1.16) est équivalente à \(g(\rho_l)=g(\rho_r)=0\) et l'inégalité (1.1.17) est équivalente à \(h(\rho_r)-h(\rho_l)\leq 0\text{.}\) On commence par intégrer \(h\) on a donc

\begin{equation*} I=\int_{\rho_l}^{\rho_r} h^{'}(v) dv= \int_{\rho_l}^{\rho_r} \zeta^{'}(v)-\sigma\eta^{'}(v) dv \end{equation*}

On utilise le fait que \(\zeta^{'}=\eta^{'}F^{'}\) et on factorise \(\zeta^{'}(v)-\sigma\eta^{'}(v)\) par \(\zeta^{'}\) pour obtenir

\begin{equation*} I=\int_{\rho_l}^{\rho_r} \eta^{'}(v)g^{'}(v)dv \le 0 \end{equation*}

puisque \(I=h(\rho_r)-h(\rho_l)\leq 0\text{.}\) On va réécrire \(I\) sous la forme:

\begin{equation*} I=\int_{\rho_l}^{\rho_r} (\eta(v)-\alpha v-\beta)^{'}(v)g^{'}(v)dv \le 0 \end{equation*}

On peut se permettre cette manipulation, car \(\int_{\rho_l}^{\rho_r} \alpha g^{'}(v)dv=\alpha(g(\rho_r)-g(\rho_l))=0\) par construction de \(g\text{.}\) Dans cette réécriture \(\alpha\) et \(\beta\) sont arbitraires. On commence par les choisir de façon à ce que la fonction \((\eta(v)-\alpha v-\beta)\) soit nulle aux bornes de l'intégrale considérée. Maintenant on reprend \(I\) et on intègre par partie ce qui donne

\begin{equation*} I=-\int_{\rho_l}^{\rho_r} (\eta(v)-\alpha v-\beta)(v)g^{''}(v)dv \le 0 \end{equation*}

grâce à ce choix particulier de \(\alpha\) et \(\beta\text{.}\) En notant que \(g^{''}=f^{''}\) on obtient

\begin{equation*} I=\int_{\rho_l}^{\rho_r} (-\eta(v)+\alpha v+\beta)(v)f^{''}(v)dv \le 0 \end{equation*}

On rappelle que par stricte convexité du flux on a \(f^{''}(v)>0\text{.}\) La fonction \((-\eta(v)+\alpha v+\beta)\) est strictement concave, car \(\eta\) est strictement convexe, elle s'annule en \(\rho_l\) et \(\rho_r\) elle est donc positive pour les valeurs entre \(min(\rho_l,\rho_r)\) et \(max(\rho_l,\rho_r)\text{.}\) On a donc un terme positif dans l'intégrale et donc l'intégrale est négative seulement si \(\rho_l \ge \rho_r\text{.}\)

Proposition 1.1.16. Condition de Oleinik.

On suppose un flux \(f\) qui est differentiable. On suppose que \((\sigma,\rho_l,\rho_r)\) une discontinuité entropique au sens de (1.1.16) (1.1.17). Il existe deux cas:

\(\rho_r \lt \rho_l\text{:}\) alors le graphe du flux \(f\) est au-dessous de la corde de la fonction \(v: k(v):f(\rho_r)+\sigma(v-\rho_r), \quad \forall \rho_r \le v \le \rho_l\)
\(\rho_r \gt \rho_l\text{:}\) alors le graphe du flux \(f\) est au-dessous de la corde de la fonction \(v: k(v):f(\rho_r)+\sigma(v-\rho_r), \quad \forall \rho_l \le v \le \rho_r\)

Preuve.

A faire en TD.

Le critère d'Oleinik dans le cas \(C^2\) et strictement convexe nous donne que \(\rho_l \ge \rho_r\text{.}\) On parle du critère de Lax.

On voit que le caractère entropique permet d'ajouter des contraintes sur les discontinuités admissibles. En utilisant le critère de Lax sur la solution faible (1.1.12) - (1.1.13) on voit qu'elle n'est plus solution. En pratique le critère entropique permet de sélectionner une discontinuité admissible et donc de récupérer l'unicité de la solution.

Théorème 1.1.17.

Soit une condition initiale \(\rho_0\in L^{\infty}(\mathbb{R};[a,b])\text{.}\) Le Problème de Cauchy (1.1.1) admet une unique solution faible entropique (1.1.15).

Preuve.

Admis

Pour finir on va introduire un problème particulier qui est central pour les lois de conservation: le problème de Riemann.

Définition 1.1.18.

Un problème de Riemann correspond au problème de Cauchy (1.1.1) avec

\begin{equation} \rho(x,0)= \begin{cases} \rho_l,\quad x \lt 0\\ \rho_r,\quad x \gt 0 \end{cases}\tag{1.1.20} \end{equation}

et ici on considérera \(f(\rho)\) strictement convexe.

Lemme 1.1.19.

La solution entropique du problème de Riemann et (1.1.1)-(1.1.20) est unique et est donnée par

\begin{equation} \rho(t,x)=\left\{\begin{array}{l} \rho_l,\quad x-S t \lt 0\\ \rho_r,\quad x-S t \gt 0 \end{array}\right.\tag{1.1.21} \end{equation}

si \(\rho_l \gt \rho_r\) avec \(S= \frac{f(\rho_r)-f(\rho_l)}{\rho_r-\rho_l}\) et

\begin{equation} \rho(t,x)=\begin{cases} \rho_l,\quad \frac{x}{t}\leq f^{'}(\rho_l)\\ (f^{'})^{-1}\frac{x}{t},\quad f^{'}(\rho_l) \lt \frac{x}{t} \lt f^{'}(\rho_r)\\ \rho_r,\quad \frac{x}{t} \geq f^{'}(\rho_r) \end{cases}\tag{1.1.22} \end{equation}

si \(\rho_l \leq \rho_r\)

Preuve.

A faire en TD.

Dans le premier cas on parle d'un choc qui se propage a vitesse S et dans le second cas on parle d'une onde de détente. De façon général, les solutions du système hyperbolique des chocs, des détentes et aussi ce qu'on appelle des ondes de contact (que l'on ne retrouve pas pour l'équation de Burgers).

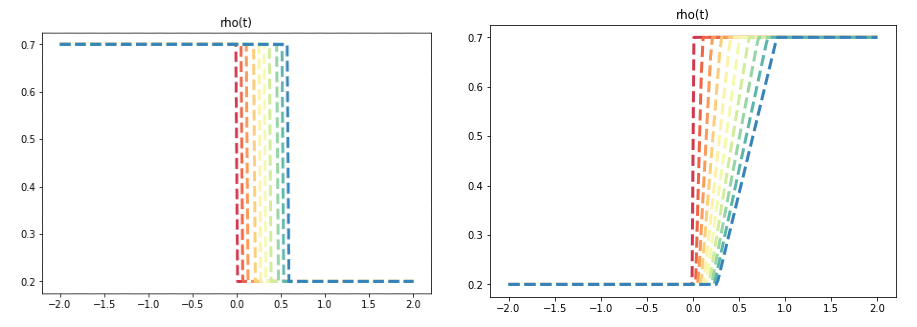
Figure 1.1.20. Problème de Riemann pour l'équation de Burgers. Gauche: \(r_l\gt r_r\text{.}\) Droite: \(r_l \lt r_r\text{.}\) On peut retrouver le notebook ici ¹.

Dans la suite du cours, on va considérer deux exemples simples de loi de conservation: l'équation de transport et l'équation de Burgers. On rajoutera un terme de viscosité. Il y aura donc pas de chocs. Cependant lorsque le terme de viscosité sera proche de zéro on retrouvera un comportement fortement nonlinéaire avec des solutions très proches de discontinuités. Ici on va considère le problème final suivant: On se donne le domaine \([0,L]\text{.}\)

Soit \(\rho(t,x)\) solution de

\begin{equation} \left\{\begin{array}{l} \partial \rho +\partial_x f(\rho)=\frac{1}{R_e}\partial_{xx} \rho\\ \rho(0,x)=\rho(x,\alpha)\\ \rho(t,x=0)=r_l, \quad \rho(t,x=L)=r_r \end{array}\right. \tag{1.1.23} \end{equation}

avec \(\alpha\in [a,b]\) une paramétrisation de la condition initiale et \(R_e\in [c,d]\) le nombre de Reynolds. L'enjeu va être de construire un modèle réduit valide pour toutes valeurs de \(\alpha\) et \(R_e\) dans les intervaux considérés.

../../../../CodeFrench.html#SciML