Méthodes de volumes finis pour les lois scalaires

Section 1.2 Méthodes de volumes finis pour les lois scalaires

On va maintenant introduire la discrétisation classique pour ce type de problème. Il s'agit de la méthode des volumes finis.

Subsection 1.2.1 Méthodes des volumes finis

Les méthodes de réduction d'ordre que nous introduirons par la suite utilisent des "snapshots" donc des exemples de simulations pour construire les modèles réduits. Il faut donc être capable de résoudre le problème d'origine. On va donc introduire des méthodes numériques pour les lois de conservations introduites précédemment (1.1.1). On ne détaillera pas les méthodes types éléments finis peu utilisées pour les lois de conservations. La méthode des volumes finis est la méthode principale pour résoudre des lois de conservation nonlinéaire. Elle utilise la propriété de conservation des équations. Elle est considérée comme très robuste, mais peu précise. On considère un maillage 1D composée de \(n+1\) noeuds \(n\) et de \(n\) mailles. On appelle \(x_j\) avec \(j\in\left\{1,N\right\}\) les centres de chaque maille et \(x_{j\pm\frac12}\) les noeuds qui forment l'interface gauche et droite de la maille \(j\text{.}\) Pour construire la méthode, on commence par intégrer l'équation dans la maille \(\Omega_j\text{.}\) On obtient

\begin{equation} \partial_t \int_{x_{j-\frac12}}^{x_{j+\frac12}} \rho dx + \int_{x_{j-\frac12}}^{x_{j+\frac12}}\partial_x\left(\frac{\rho^2}{2} \right)dx =\frac{1}{R_e}\int_{x_{j-\frac12}}^{x_{j+\frac12}}\partial_{xx}\rho dx\tag{1.2.1} \end{equation}

Afin de pouvoir écrire un schéma on va définir le degré de liberté de la méthode. Ici il s'agit de choisir la valeur moyenne de \(\rho\) dans chaque maille:

\begin{equation*} \rho_j(t)=\frac{1}{\Delta x_j}\int_{x_{j-\frac12}}^{x_{j+\frac12}} \rho dx \end{equation*}

On va donc construire une approximation constante par maille. Une fois ce degré de liberté définit l'équation (1.2.1) se réécrit en utilisant le théorème de Green qui relie l'intégrale d'une divergence à une intégrale de bord. On obtient

\begin{equation} \Delta x\partial_t\rho_j(t) + \left( f(\rho)(x_{j+\frac12})-f(\rho)(x_{j-\frac12}) \right)=\frac{1}{R_e}\left( (\partial_x\rho)(x_{j+\frac12})-(\partial_x\rho)(x_{j-\frac12}) \right)\tag{1.2.2} \end{equation}

Cependant écrit comme cela le système n'est pas fermé, car nous obtenons une relation entre valeurs moyennes et valeurs ponctuelles, mais qui ne nous permet pas de calculer l'une ou l'autre. Pour fermer le problème, on propose l'approximation suivante:

\begin{equation} f(\rho)(x_{j+\frac12})\approx g(\rho_j,\rho_{j+1})\tag{1.2.3} \end{equation}

\begin{equation} f(\partial_x\rho)(x_{j+\frac12})\approx g_d(\rho_j,\rho_{j+1})\tag{1.2.4} \end{equation}

On appelle \(g(\rho_l,\rho_r)\) et \(g_d(\rho_l,\rho_r)\) des flux numériques qui modélise le flux d'information entre deux unités de volumes (ici les mailles).

Définition 1.2.1.

Un flux est dit consistant pour l'équation (1.1.1) si

\begin{equation*} g(\rho,\rho)=f(\rho) \end{equation*}

Tout l'enjeu de la méthode des volumes finis est de construire ce flux numérique. Le choix le plus naturel est de choisir les flux suivants:

\begin{equation} g_{j+\frac12}=g(\rho_j,\rho_{j+1})=\frac{1}{2}(f(\rho_j)+f(\rho_{j+1})) = f(\rho(x_{j+\frac12}))+O(\Delta x^2) \tag{1.2.5} \end{equation}

\begin{equation} g_{d,j+\frac12}=g_d(\rho_j,\rho_{j+1})=\frac{\rho_{j+1}-\rho_{j} }{\Delta x}=(\partial_x\rho)(x_{j+\frac12})+O(\Delta x^2)\tag{1.2.6} \end{equation}

Pour le premier flux, la consistance se retrouve formellement avec la méthode du point milieu en intégration. La seconde se retrouve à l'aide de développement de Taylor comme vu avec les différences finies (voir cours de rappel)

Lemme 1.2.2.

Quelque soit le flux numérique utilisé dans le schéma discret en espace et continue en temps, on peut écrire cela sous la forme:

\begin{equation*} \Delta x\partial_t\rho_j(t) + \left( g_{j+\frac12}-g_{j-\frac12} \right)=\frac{1}{R_e}\left(g_{d,j+\frac12}-g_{d,j-\frac12} \right) \end{equation*}

on obtient formellement:

\begin{equation*} \partial_t \sum_{j\in \mathbb{Z}}\rho_j(t)=0 \end{equation*}

On parle de schémas conservatifs.

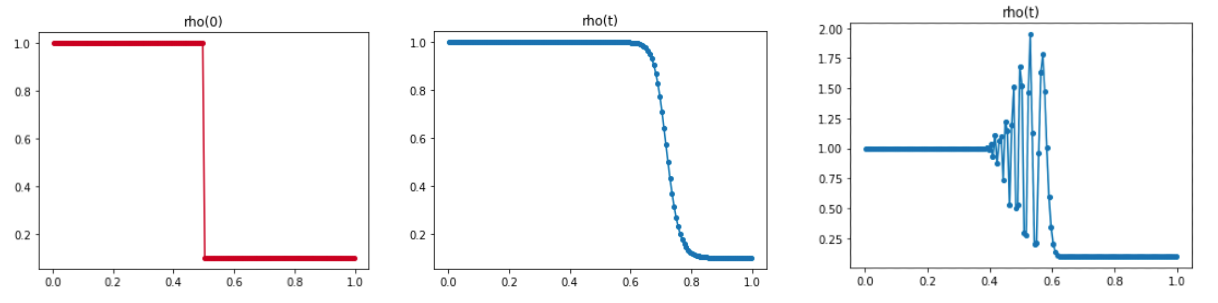
Figure 1.2.3. Schéma de volumes finis centré pour l'équation de Burgers ou d'advection en fonction du Reynolds. Gauche: Condition initiale. Milieu: Exemple avec \(R_e=100\text{.}\) Droite: Exemple avec \(R_e=10000\text{.}\) On peut retrouver le notebook ici ¹.

Les résultats numériques précédemment montrent une instabilité lorsque le Reynolds est trop petit. Cela vient du fait que fondamentament le flux dit centré (1.2.5) est instable. Cela peut se régler avec un schéma implicite, mais les résultats restent très mauvais lorsqu'on une discontinuité apparaît. Pour traiter les régimes avec de grand Reynolds (voir sans viscosité) qui génère des chocs il faut des flux adaptés pour la partie hyperbolique. C'est ce qu'on va rapidement introduire maintenant. On considérera pour les moments le modèle sans terme dissipatif. Dans la suite, on va considérer une loi de conservation scalaire générale de type (1.1.1). Comme on vient de le voir, le schéma devient instable lorsque la dissipation physique devient trop petite. Une idée naturelle sera donc d'ajouter de la dissipation au schéma centrée et de la construire minimale pour assurer la stabilité.

On considère le flux générique (flux de Lax-Friedrich global):

\begin{equation} g_{j+\frac12}(\rho_j,\rho_{j+1})=\frac12\left(f(\rho_j)+f(\rho_{j+1})\right) +\frac{c}{2}(\rho_j-\rho_{j+1})\tag{1.2.7} \end{equation}

Le second terme de \(g_{j+\frac12} \) revient a ajouter une viscosité au schéma centré de coefficient \(\frac{c\Delta x}{2}\text{.}\) On voit bien que ce choix assure une consistance à l'ordre un puisque le schéma centré est consistant à l'ordre deux. Maintenant la question de savoir commet choisir \(c\) ?

Pour le problème linéaire qui conserve la norme \(L^2\) on assure la stabilité en faisant décroître la norme \(L^2\) discrète. La conservation n'est pas possible à cause des erreurs d'arrondis. Il nous faut un équilavent en nonlinéaire. Pour les lois de conservations de type (1.1.1) on sait que les solutions entropiques satisfont

\begin{equation*} \partial_t \eta(\rho) + \partial_x \zeta(\rho) = 0 \end{equation*}

pour les solutions régulières et

\begin{equation*} \partial_t \eta(\rho) + \partial_x \zeta(\rho) \leq 0 \end{equation*}

de façon générale. L'idée est d'essayer de préserver cette propriété au niveau discret afin de capturer les solutions entropiques.

Définition 1.2.4.

Soit l'équation (1.1.1) muni du couple entropie - flux entropique \((\eta,\zeta))\text{.}\) Soit un flux numérique associé \(g_{j+\frac12}(\rho_j,\rho_{j+1})\) tel que

\begin{equation} \frac{\rho_{j}^{n+1}-\rho_{j}^{n}}{\Delta t}+\frac{g_{j+\frac12}-g_{j-\frac12}}{\Delta x}=0, \quad \forall j\in \left\{1,N\right\}\tag{1.2.8} \end{equation}

Le schéma associé à ce flux est dit entropique si et seulement si il existe une flux entropique \(\zeta_{j+\frac12}(\rho_j,\rho_{j+1})\) tel que

\begin{equation} \frac{\eta(\rho_{j}^{n+1})-\eta(\rho_{j}^{n})}{\Delta t}+\frac{\zeta_{j+\frac12}-\zeta_{j-\frac12}}{\Delta x}\leq 0, \quad \forall j\in \left\{1,N\right\}\tag{1.2.9} \end{equation}

Proposition 1.2.5.

On définit

\begin{equation*} m=inf_{1 \le j \le N}(\rho_j^0),\quad M=sup_{1\le j \le N}(\rho_j^0)\text{.} \end{equation*}

On suppose que \(\forall \rho\in [m,M], \quad f^{'}(\rho)\ge 0\text{.}\)

Si \(\frac{c\Delta t}{\Delta x}\le 1\) et \(\underset{m\le x\le M}{max}\mid f^{'}(x)\mid \leq c\) alors la solution donnée par (1.2.8) satisfait

\begin{equation} m\le \rho_j^{n+1}\le M , \quad \forall j\in \left\{1,N\right\}\tag{1.2.10} \end{equation}

et si \(\frac{c\Delta t}{\Delta x}\le \frac12\) elle satisfait aussi l'inégalité d'entropie (1.2.9) avec

\begin{equation} \zeta_{j+\frac12}=\frac{\zeta(\rho_{j+1})+\zeta(\rho_j)}{2}+\frac{c}{2}(\eta(\rho_j^n)- \eta(\rho_{j+1}^n))\tag{1.2.11} \end{equation}

Preuve.

Démonstration du principe du maximum:

On écrit le temps \(n+1\) en fonction du temps \(n\text{.}\) On obtient

\begin{equation} \rho_j^{n+1}=\rho_j^n+\frac{c\Delta t}{2\Delta x}(\rho_{j+1}^n-2\rho_j^n+\rho_{j-1}^n)- \frac{\Delta t}{2\Delta x}[f(\rho_{j+1}^n)-f(\rho_{j-1}^n)]\tag{1.2.12} \end{equation}

\begin{equation} \rho_j^{n+1}=\rho_j^n+\frac{c\Delta t}{2\Delta x}(\rho_{j+1}^n-2\rho_j^n+\rho_{j-1}^n)- \frac{\Delta t}{2\Delta x}[a_j^n(\rho_{j+1}^n-\rho_{j-1}^n)]\tag{1.2.13} \end{equation}

avec \(a_j^n=\frac{f(\rho_{j+1}^n)-f(\rho_{j-1}^n)}{(\rho_{j+1}^n-\rho_{j-1}^n)}\text{.}\) Par le théorème des accroissements finis il existe un \(b_j^n\) tel que

\begin{equation*} a_j^n=f^{'}(b_j^n), \quad min(\rho_{j-1}^n,\rho_{j+1}^n))\le b_j^n \le max(\rho_{j-1}^n,\rho_{j+1}^n)) \end{equation*}

Maintenant on réécrit (1.2.13) ce qui donne

\begin{equation} \rho_j^{n+1}=[1-\frac{c\Delta t}{\Delta x}]\rho_{j}^n +\frac{\Delta t}{2\Delta x}[c-a_j^n]\rho_{j+1}^n+\frac{\Delta t}{2\Delta x}[c+a_j^n]\rho_{j-1}^n\tag{1.2.14} \end{equation}

La condition CFl assure que \([1-\frac{c\Delta t}{\Delta x}]>0\text{.}\) La condition sur \(c\) assure que \((c\pm a_j^n)>0\text{.}\) On a donc une combinaison convexe donc

\begin{equation} min(\rho_{j-1}^n,\rho_{j}^n,\rho_{j+1}^n) \le \rho_j^{n+1}\le max(\rho_{j-1}^n,\rho_{j}^n,\rho_{j+1}^n)\tag{1.2.15} \end{equation}

En itérant en temps, on conclut.
Démonstration de la propriété d'entropie

On commence par réécrire le schéma en posant \(\nu = \frac{\Delta t}{\Delta x}\) afin d'obtenir

\begin{equation*} \rho_j^{n+1}=\frac12(\rho_j^n+\nu c(-\rho_j^n+\rho_{j-1}^n) -\nu (f(\rho_j^n)-f(\rho_{j-1}^n)) ) + \frac12(\rho_j^n+\nu c(\rho_{j+1}^n-\rho_{j}^n) -\nu (f(\rho_{j+1}^n)-f(\rho_{j}^n)) ) \end{equation*}

Par convexité de l'entropie on obtient

\begin{equation*} \eta(\rho_j^{n+1})\le \frac12\eta(\rho_j^n+\nu c(-\rho_j^n+\rho_{j-1}^n) -\nu (f(\rho_j^n)-f(\rho_{j-1}^n)) ) + \frac12\eta(\rho_j^n+\nu c(\rho_{j+1}^n-\rho_{j}^n) -\nu (f(\rho_{j+1}^n)-f(\rho_{j}^n)) ) \end{equation*}

On peut réarranger les termes afin de faire apparaître l'inégalité qu'on souhaite. Dans ce cas on obtient

\begin{equation} \eta(\rho_{j}^{n+1})-\eta(\rho_{j}^{n})+\nu(\zeta_{j+\frac12}-\zeta_{j-\frac12})\leq \frac{1}{2}(\psi_{-}(\rho_{j-1}^n)+\psi_{+}(\rho_{j+1}^n))\tag{1.2.16} \end{equation}

avec

\begin{equation*} \phi_{+}(\rho)=\eta(\rho+\nu c(\rho -\rho_j^n) -\nu (f(\rho) - f(\rho_j^n)) \end{equation*}

\begin{equation*} -\eta(\rho_j^n)-\nu c (\eta(\rho)-\eta(\rho_j^n))+\nu (\zeta(\rho)-\zeta(\rho_j^n)) \end{equation*}

et

\begin{equation*} \phi_{-}(\rho)=\eta(\rho+\nu c( -\rho_j^n+\rho) -\nu (-f(\rho) + f(\rho_j^n)) \end{equation*}

\begin{equation*} -\eta(\rho_j^n)-\nu c (\eta(\rho)-\eta(\rho_j^n))+\nu (-\zeta(\rho)+\zeta(\rho_j^n)) \end{equation*}

Pour conclure il suffit donc de montrer que les deux fonctions \(\phi_{\pm}\) sont négatives. Puisque qu'on sait qu'elles sont nulles en \(\rho_j^n\) on va donc montrer qu'elles sont croissantes \(\rho_j^n\) gauche de zéro et donc décroissante à droite de \(\rho_j^n\text{.}\) On commence par \(\phi_{+}\text{.}\) La dérivée de \(\phi_{+}\) est donné par

\begin{equation*} \phi_{+}^{'}(\rho)=\nu(c-f^{'}(\rho))\underbrace{[\eta^{'}(\rho_j^n+\nu c(\rho -\rho_j^n)-\nu(f(\rho)-f(\rho_j^n))) -\eta^{'}(\rho)]}_{A} \end{equation*}

En utilisant la définition de \(c\) on obtient que le premier terme soit positif. On va donc se concentrer sur le terme \(A\) que l'ont va réécrire a l'ai des accroissements finis

\begin{equation*} A=\eta^{''}(a)(\rho_j^n+\nu c(\rho -\rho_j^n)-\nu(f(\rho)-f(\rho_j^n)) -\rho) \end{equation*}

avec \(min(\rho,\rho^*) \lt a \lt max(\rho,\rho^{*})\) et \(\rho^{*}=\rho_j^n+\nu c(\rho -\rho_j^n)-\nu(f(\rho)-f(\rho_j^n)\text{.}\) La convexité de \(\eta\) permet d'obtenir que \(\eta^{''}(a)\) est positive. On va réécrire le second terme à l'aide d'accroissement fini sur \(f\)

\begin{equation*} A=\eta^{''}(a)(1-\nu c +\nu f^{'}(b))(\rho_j^n-\rho) \end{equation*}

avec \(min(\rho_j^n,\rho) \le b \le max(\rho_j^n,\rho)\text{.}\) Puisque \(\mid f^{'}(b)\mid \lt c \) on a donc \((1-\nu c +\nu f^{'}(b)) \gt 0\) si la CFL plus stricte (avec le \(\frac12\)) est respectée. Par conséquent

\begin{equation*} \phi_{+}^{'}(\rho)=C(\rho)(\rho_j^n-\rho) \end{equation*}

avec \(C(\rho) \ge 0\text{.}\) On voit donc que si \(\rho \lt \rho_j^n\) la fonction \(\phi_{+}\) est croissante et si \(\rho \gt \rho_j^n\) elle est décroissante. Puisqu’elle est nulle en \(\rho_j^n\) elle est donc toujours négative. Pour \(\phi_{-}\) le principe est le même. On commence par écrire la dérivée

\begin{equation*} \phi_{-}^{'}(\rho)=\nu(c+f^{'}(\rho))\underbrace{[\eta^{'}(\rho_j^n+\nu c(\rho -\rho_j^n)-\nu(f(\rho_j^n)-f(\rho))) -\eta^{'}(\rho)]}_{B} \end{equation*}

Le premier terme est positif et le second s'écrit

\begin{equation*} B=\eta^{''}(a)(1-\nu c -\nu f^{'}(b))(\rho_j^n-\rho) \end{equation*}

À partir de là on peut appliquer le même raisonnement et conclure.

Ce résultat s'interprète comme un résultat de stabilité du schéma numérique. Il est l'extension nonlinéaire de la décroissance en norme qui assure la stabilité des schémas linéaires. Un schéma peut être stable sans être entropique, mais cette propriété assure une forme assez forte de stabilité.

Théorème 1.2.6. (théorème de Lax Wendroff).

On considère \(u_h\) la solution du schéma (1.2.8) - (1.2.7) avec une condition initiale \(\rho_0 \in L^{\infty}(\mathbb{R})\text{.}\) On suppose que la condition CFL \(\frac{c\Delta t}{\Delta x}\le \frac12\) est satisfaite. Supposons qu'il existe \(\rho\in L_{loc}^1(\mathbb{R}^{+}\times \mathbb{R})\) tel que

\begin{equation*} \underset{(\Delta x,\Delta t)\rightarrow 0}{\operatorname{lim}}\Norm \rho_h -\rho \Norm_{L_{loc}^1(\mathbb{R}^{+}\times \mathbb{R})}=0 \end{equation*}

\begin{equation*} \underset{(\Delta x,\Delta t)\rightarrow 0}{\operatorname{lim}}\Norm \rho_h(0,.) -\rho_0 \Norm_{L_{loc}^1(\mathbb{R})}=0 \end{equation*}

et que \(c\) est borné alors \(\rho\in L^{\infty}(\mathbb{R}^{+}\times \mathbb{R})\) est une solution faible entropique.

Preuve.

Puisque qu'on suppose que la condition CFL est vérifiée alors en utilisant (1.2.10) on obtient une majoration du type

\begin{equation*} \Norm \rho_{\Delta x,\Delta t}\Norm_{L^{\infty}(\mathbb{R}^{+}\times \mathbb{R})}\leq \Norm \rho_0\Norm_{L^{\infty}(\mathbb{R})} \end{equation*}

On prend une fonction \(C_0^{\infty}\) (à support compact). On pense ensuite \(\phi_j^n=\phi(n\Delta t,j\Delta x)\text{.}\) On introduit l'intégrale discrète de notre équation multipliée par la fonction test

\begin{equation} \sum_{j,n}\left( \frac{\rho_j^{n+1}-\rho_j^n}{\Delta t}+\frac{f_{j+\frac12} - f_{j-\frac12}}{\Delta x}\right)\phi_j^n \Delta x\Delta t=0\tag{1.2.17} \end{equation}

Maintenant on va appliquer une intégration par partie discrète ce qui revient a un rearrangement des termes:

\begin{equation} -\sum_{j,n}\left(\rho_j^n\frac{\phi_j^n-\phi_j^{n-1}}{\Delta t}+ f_{j+\frac12}\frac{\phi_{j+1}^n-\phi_j^{n}}{\Delta x}\right)\Delta t \Delta x -\sum_{j}\rho_j^0\phi_j^0\Delta x\tag{1.2.18} \end{equation}

On va considérer le premier terme. On peut le réécrire sous forme intégrale:

\begin{equation*} \sum_{j,n}\rho_j^n\frac{\phi_j^n-\phi_j^{n-1}}{\Delta t}\Delta x\Delta t=\int\int \rho_{\Delta x,\Delta t} v_{\Delta x,\Delta t}dxdt \end{equation*}

avec \(v_{\Delta x,\Delta t}=\frac{\phi_j^n-\phi_j^{n-1}}{\Delta t} \chi_{x\in \Omega_j}\chi_{t\in [t_n,t_{n+1}]}\text{.}\) Puisque \(\phi\) est \(C_0^{\infty}\) on a une convergence uniforme de \(v_{\Delta x,\Delta t}\) vers la dérivée de \(\phi\) et puis que \(\rho_{\Delta x,\Delta t}\) converge dans \(L_{loc}^1\)donc

\begin{equation*} \rho_{\Delta x,\Delta t}v_{\Delta x,\Delta t}\rightarrow \rho\partial_{t}\phi \end{equation*}

dans \(L_{loc}^1\text{.}\) Puisque \(\phi\) est infiniment dérivable à support compact alors on \(\partial_{t}\phi\) qui est borné et donc

\begin{equation*} \Norm \rho_{\Delta x,\Delta t} v_{\Delta x,\Delta t}\Norm_{L^{\infty}(\mathbb{R}^{+}\times \mathbb{R})}\leq M\Norm \rho_0\Norm_{L^{\infty}(\mathbb{R})} \end{equation*}

On applique donc le Théorème de convergence dominée de Lebesgue ce qui nous donne

\begin{equation*} \int\int \rho_{\Delta x,\Delta t}v_{\Delta x,\Delta t} \underset{\Delta x \rightarrow 0}{\rightarrow }\rho\partial_{t}\phi dx dt \rightarrow \int\int \rho \partial_t \phi dx dt \end{equation*}

donc

\begin{equation} \sum_{j,n}\rho_j^n\frac{\phi_j^n-\phi_j^{n-1}}{\Delta t}\Delta x\Delta t \underset{\Delta x \rightarrow 0}{\rightarrow }\int\int \rho \partial_t \phi dx dt\tag{1.2.19} \end{equation}

Avec le même argument on obtient que

\begin{equation} \sum_{j}\rho_j^n \phi_j^n \Delta x \rightarrow \int_{\mathbb{R}}\rho_0(x)\phi(x)dx\tag{1.2.20} \end{equation}

On va passer au dernier terme:

\begin{equation*} \sum_{j,n}f_{j+\frac12}\frac{\phi_{j+1}^n-\phi_j^{n}}{\Delta x}\Delta t \Delta x= A + B \end{equation*}

avec

\begin{equation*} A= \sum_{j,n}f(\rho_j^n)\frac{\phi_{j+1}^n-\phi_j^{n}}{2\Delta x}\Delta t \Delta x \end{equation*}

\begin{equation*} B= c\sum_{j,n}\rho_j^n \frac{-\phi_{j+1}^n+2\phi_j^{n}-\phi_{j-1}^{n}}{2\Delta x}\Delta t \Delta x \end{equation*}

On pose \(f_{\Delta x,\Delta t}=f(\rho_j^n)\chi_{x\in \Omega_j}\chi_{t\in [t_n,t_{n+1}]}\text{.}\) Avant de pouvoir traiter ce terme comme précédemment il faut montrer qu'il converge vers \(f(\rho(t,x))\text{.}\) Pour cela il suffit de remarquer que:

\begin{equation*} \mid f_{\Delta x,\Delta t} - f(\rho(t,x)) \mid \le \operatorname{\mid f^{'}\mid }\mid \rho_{\Delta x,\Delta t}- \rho(t,x)\mid \end{equation*}

donc

\begin{equation*} \int \int\mid f_{\Delta x,\Delta t} - f(\rho(t,x)) dx dt \mid \le \operatorname{\mid f^{'}\mid }\mid \int \int\rho_{\Delta x,\Delta t}- \rho(t,x)\mid dx dt \end{equation*}

On a donc convergence \(f_{\Delta x,\Delta t}\) vers \(f(\rho(t,x))\) dans \(L_{loc}^1\) par convergence de \(\rho_{\Delta x,\Delta t}\) dans \(L_{loc}^1\text{.}\) À partir de la, on utilise les mêmes arguments (convergence uniforme de \(\phi\text{,}\) convergence dominée, etc) pour obtenir

\begin{equation} A=\sum_{j,n}f(\rho_j^n)\frac{\phi_{j+1}^n-\phi_j^{n}}{\Delta x}\Delta x\Delta t\underset{\Delta x \rightarrow 0}{\rightarrow } \int\int f(\rho)\partial_x \phi dx dt\tag{1.2.21} \end{equation}

Maintenant il faut s'occuper du terme \(B\text{.}\) On commence par réécrire ce terme

\begin{equation*} B= \frac{c\Delta x}{2}\sum_{j,n}\rho_j^n \frac{-\phi_{j+1}^n+2\phi_j^{n}-\phi_{j-1}^{n}}{\Delta x^2}\Delta t \Delta x \end{equation*}

Ensuite on utilise le fait que la dérivée seconde de \(\phi\) est bornée par la norme du vecteur \(\phi_j\) car il s’agit d'une fonction à. La fonction \(\phi\) étant infiniment dérivable et a support compact on peut borner ce vecteur uniformément. On peut donc uniformément borner la somme dans \(B\) car la solution \(\rho_{\Delta t,\Delta x}\) est bornée sous CFL. Par conséquent

\begin{equation*} B\underset{\Delta x \rightarrow 0}{\rightarrow 0} \end{equation*}

En utilisant (1.2.18) - (1.2.19) - (1.2.20) et (1.2.21). On obtient que notre somme (1.2.17) converge vers une solution faible. Pour monter que notre solution est entropique on part de

\begin{equation} \sum_{j,n}\left( \frac{\eta(\rho_j^{n+1})-\eta(\rho_j^n)}{\Delta t}+ \frac{\zeta_{j+\frac12} - \zeta_{j-\frac12}}{\Delta x}\right)\phi_j^n \Delta x\Delta t\le 0\tag{1.2.22} \end{equation}

On utilise les mêmes arguments qu’au-dessus avec le fait que ma fonction test est positive pour obtenir que la convergence vers la solution entropique.

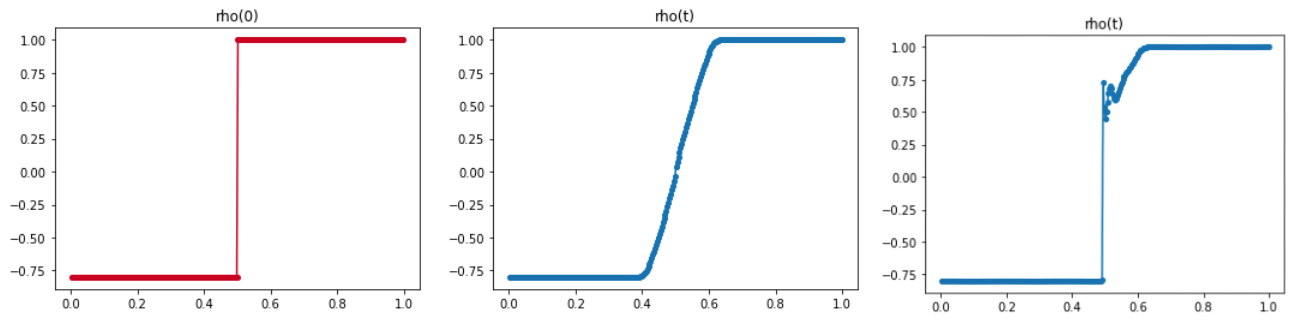
Figure 1.2.7. Schéma de volumes finis entropique ou non pour l'équation de Burgers. Gauche: schéma entropique. Droite: schéma non entropique. On peut retrouver le notebook ici ².

Sur la figure Figure 1.2.7 on compare un schéma entropique et un schéma non entropique pour calculer une détente pour l'équation de Burgers. On remarque que dans tous les cas le schéma entropique capture une solution de type détente. Par contre si la condition initiale passe par zéro on voit que le schéma non entropique capture un un choc stationnaire au lieu d'une détente.

Il existe beaucoup d'autres schémas comme le schéma de Godunov qui utilise la solution du problème de Riemann ou le schéma de Osher qui utilise une approche de type décentrée. Dans l'ensemble des cas, les schémas introduisent de la dissipation homogène à \(O(\Delta x)\text{.}\)

Subsection 1.2.2 Schémas en temps

Plusieurs schémas en temps peuvent être couplés avec les schémas de types volumes finis, éléments finis. On va rapidement rappeler les principales familles qui sont utilisées et qui seront aussi utilisées pour les modèles réduits. On se propose d'écrire les schémas sous une forme particulière qui nous sera utile pour la suite. Ici on résout une ODE du type

\begin{equation} \frac{d \bs{x}}{dt}=\bs{f}(\bs{x}(t))\tag{1.2.23} \end{equation}

Elle peut être issue de la discrétisation d'une EDP.

Subsubsection 1.2.2.1 Méthodes de Runge-Kutta

Les méthodes de Runge-Kutta sont des méthodes d'ordre élevées qui calculent le le temps courant uniquement à partir du temps précédent. Cependant elle calculent les quantités et les flux à des temps intermédiaires.

Définition 1.2.8. Méthodes de Runge-Kutta.

La méthode de Runge Kutta s'écrit en deux étapes: une première ou on calcul un résidu solution de:

\begin{equation} \bs{r}_{i}^{n}\left(\bs{w}_{1}^{n}, \ldots, \bs{w}_{s}^{n}\right)=0, \quad i \in \mathbb{N}(s)\tag{1.2.24} \end{equation}

avec

\begin{equation} \bs{r}_{i}^{n}\left(\bs{w}_{1}, \ldots, \bs{w}_{s}\right) :=\bs{w}_{i}-\bs{f}\left(\bs{x}^{n-1} +\Delta t \sum_{j=1}^{s} a_{i j} \bs{w}_{j}, t^{n-1}+c_{i} \Delta t\right), \quad i \in \mathbb{N}(s)\tag{1.2.25} \end{equation}

et ensuite on en déduit la solution

\begin{equation} \bs{x}^n=\bs{x}^{n-1}+\Delta t \sum_{i=1}^s b_i \bs{w}_i^n \tag{1.2.26} \end{equation}

Subsubsection 1.2.2.2 Méthodes temporelles multi-pas

Il s'agit de méthodes qui utilisent l'approximation à plusieurs pas de temps. Ici on va considérer les méthodes explicites.

Définition 1.2.9. Méthodes linéaires multi-pas.

Une méthode linéaire a \(k\) pas s'écrit en deux étapes: une première ou on calcul un résidu solution de:

\begin{equation} \bs{r}\left(\bs{w}\right)=0\tag{1.2.27} \end{equation}

avec

\begin{equation} \bs{r}(\bs{w})=\alpha_0 \bs{w} - \Delta t \beta_0 \bs{f}(\bs{w},t) + \sum_{j=1}^{K} \alpha_{j} \bs{x}^{n-j}- \Delta t \sum_{j=1}^{K} \beta_{j} \bs{f}\left(\bs{x}^{n-j}, t^{n-j}\right),\tag{1.2.28} \end{equation}

avec comme condition \(\sum_{j=0}^K\alpha_j=0\) et la solution est donnée par

\begin{equation} \bs{x}_n=\bs{w} \tag{1.2.29} \end{equation}

La plus connue est la méthode d'Euler explicite ou \(K=1\) et \(\alpha_0/\beta_0=(1,0)\text{,}\) \(\alpha_1/\beta_1=(1,1)\text{.}\) La méthode d'Euler implicite correspond-elle à \(K=1\) et \(\alpha_0/\beta_0=(1,1)\text{,}\) \(\alpha_1/\beta_1=(1,0)\text{.}\) Pour finir la méthode classe de Crank-Nicolson correspond à \(K=1\) et \(\alpha_0/\beta_0=(1,\frac12)\text{,}\) \(\alpha_1/\beta_1=(1,\frac12)\text{.}\) Les méthodes dites de Adams–Bashforth, Adam-Moulton (explicites) ou BDF (implicite) rentrent dans ce cadre.

Conclusion.

Dans cette section, on a défini une classe d'EDP appelée équations hyperboliques ou loi de conservation. On a montré leurs spécificités à travers l'apparition de discontinuités et avons introduit la théorie des solutions faibles associées. On a ensuite introduit les méthodes de volumes finis pour ces EDP ainsi que leurs propriétés fondamentales. Dans un dernier temps, on a défini les schémas classiques en temps. On va maintenant aborder la question de la réduction de dimension.

../../../../CodeFrench.html#hyperbolique