Section 5.2 Réseaux de neurones convolutifs
Subsection 5.2.1 Données structurées et a priori
Si on suit les résultats théoriques précédent on voit que les réseaux de neurones totalement connectés ne permettent de briser la malédiction de la grande dimension même augmenter la profondeur semble être une solution pour améliorer les choses. Maintenant considérons des problèmes de type EDP ou de type traitement du signal. Construire une fonction capable de classifier des images ou de déterminer les contours d'une forme d'une image (segmentation). La dimension d'entrée est la taille du nombre de pixels. On voit donc qu'il va s'agir d'un problème en très grande dimension. De la même façon imaginons un réseau qui prend une fonction \(f\) discrétisée sur un maillage et renvoie la solution du problème de Laplace \(-\Delta u=f\) associé. Dans ce cas la dimension du problème est le nombre de dégré de liberté du maillage ce qui peut être la encore très important.
Cependant dans les deux cas, on supposer que la dimension réelle du problème est plus faible. En effet dans les deux cas il s'agit d'un problème structuré. Lorsqu'on regarde une image qui a du sens, les pixels voisins ne sont pas totalement indépendants. De la même façon lorsqu'on regarde une fonction continue discrétisée l'ensemble des valeurs possibles pour deux valeurs voisines est plus petit que si on regarde du bruit. Cette corrélation entre les données peut laisser supposer qu’ en pratique le problème est en dimension plus petite. Les réseaux convolutifs ont été conçus pour même de façon très basique le fonctionnement de la vision humaine. Une fois qu'on à pu remarquer leurs extrêmes efficacités on a essayé de comprendre pourquoi cela marchait aussi bien. L'iée qui est apparu c'est que finalement les réseaux convonlutifs encodent dans leurs architectures un certain nombre de propriétés de du problème qui permet de réduire drastiquement l'espace des fonctions possibles. C'est notamment l'objet des articles de S. Mallat [1.12] et des travaux en apprentissage géométrique [1.11]. On se propose de construire les réseaux convolutifs rapidement en suivant plus ses arguments.
Subsubsection 5.2.1.1 Symétrie
Le premier ingrédient qui va être utile c'est la notion de symétrie. Une symétrie est une transformation sur une donnée d'entrée d'une fonction qui va laisser inchangé le résultat de la fonction. La notion de symétrie est fondamentale pour permettre de réduire la dimension du problème. Imaginons qu'on doive déterminer une fonction \(f(\bs{x}): \mathbb{R}^2 \rightarrow \mathbb{R}^2\) tel que
avec \(A\) une matrice carrée de taille deux. On suppose que dans le problème qu'on regarde on sait que la fonction est une isométrie donc \(\parallel A \bs{x}\parallel_2 = \parallel \bs{x}\parallel_2\text{.}\) En passant en coordonnée polaire on peut montrer que cela revient à ce que \(A\) soit une matrice de rotation directe (déterminant positif) ou indirecte (déterminant négatif). On voit donc qu'il suffit de déterminer l'angle et de caractère direct ou indirect. La dimension intrasec du problème devient plutôt deux. Une idée est donc d'introduire certaines symétries du problème dans le réseau qu'on utilisera. Dans [1.11] il formalise cela pour les signaux structurés sur certains domaines (cela permet de généraliser à des données structurées autrement que sur des grilles) à l'aide de la théorie des groupes. On appelle un signal \(\mathcal{C}\)-valué sur le domaine \(\Omega\) une fonction: Chaque composante de \(\mathcal{C}\) est appelée \(canal\text{.}\) On peut y associé un espace de fonction \(L(\Omega,\mathcal{C})\) munit du produit scalaire On considère un ensemble \(\mathcal{G}\) munit d'une loi de composition interne \(\circ\) est un groupe si on satisfait les propriétés suivantes: Associativité: \(a \circ (b\circ c) = (a \circ b)\circ c,\quad \forall a,b,c\in \mathcal{G} \) Elément neutre: \(\exists e\in \mathcal{G}, \quad e \circ a = a, \forall a \in \mathcal{G} \) Inverse: \(\exists a^{-1}\in \mathcal{G}, \quad a^{-1}\circ a = e, \forall a \in \mathcal{G} \) On considère un ensemble \(\mathcal{G}\) munit d'une loi de composition interne \(\circ\) d'élément neutre \(e\text{.}\) On considère un ensemble \(\Omega\text{.}\) Un Action de groupe est une application qui satisfait et
Définition 5.22.
Définition 5.23. Groupe.
Définition 5.24. Action de Groupe.
Exemple 5.25.
Définition 5.26. Représentation de groupe.
Soit \(\mathcal{G}\) un groupe, soit \(E\) un \(\mathbb{K}\) espace vectoriel. Une une représentation de groupe est une application
avec \(GL(E)\) l'espace des endomorphismes bijectifs linéaires de \(E\) dans \(E\) qui satisfait \(\rho(g_1 g_2): \rho (g_1)\circ \rho(g_2), \quad \forall g_1,g_2\in G^2\) On écrit une action de groupe sur \(x\in E\) à travers sa représentation comme:
Proposition 5.27.
Soit un signal \(x(u):\Omega \rightarrow \mathcal{C}\) et \(\mathcal{G}\) un groupe qui agit sur \(\Omega\text{.}\) Alors l'application
est une action de groupe sur \(L(\Omega,\mathcal{C})\) l'ensemble des applications de \(\Omega\) dans\(\mathcal{C}\text{.}\) En termes de représentation on a
Preuve.
-
Propriété 1: soit \(e\) l'élément neutre de \(\mathcal{G}\)
\(e\cdot x(u)= x(e^{-1}\cdot u) = x(e \cdot x)=x(u)\) car \(\mathcal{G}\) agit sur \(\Omega\text{.}\)
-
Propriété 2: soit \(g_1,g_2\) des éléments de \(\mathcal{G}\)
D'abord
\begin{equation*} A=g_2\cdot (g_1\cdot x(u))= (g_1\cdot f)(g_2^{-1}\cdot u) = x(g_1^{-1}\cdot (g_2^{-1}\cdot u)) \end{equation*}Ensuite
\begin{equation*} B=(g_2\circ g_1)\cdot x(u)= f(g_2\circ g_1)^{-1} \cdot u) = x(( g_1^{-1 }\circ g_2^{-1}) \cdot u) \end{equation*}On démontre facilement que pour un groupe \(g_2\circ g_1)^{-1} =g_1^{-1 }\circ g_2^{-1} \text{.}\) Puisque \(\mathcal{G}\) agit sur \(\Omega\) on a
\begin{equation*} ( g_1^{-1 }\circ g_2^{-1}) \cdot u = g_1^{-1}\cdot (g_2^{-1}\cdot u) \end{equation*}donc \(A=B\) ce qui conclut la preuve.
Définition 5.28. Invariance.
On se donne une fonction \(f: L(\Omega,\mathcal{C}) \rightarrow V\) qui transforme un signal. Cette fonction est dit \(\mathcal{G}\)-invariante si \(\forall g\in \mathcal{G}\) et \(\forall x\in L(\Omega,\mathcal{C})\) un signal on a
Définition 5.29. Equivariance.
On se donne une fonction \(N: L(\Omega,\mathcal{C}) \rightarrow V\) qui transforme un signal. Cette fonction est dit \(\mathcal{G}\)-equivariante si \(\forall g\in \mathcal{G}\) et \(\forall x\in L(\Omega,\mathcal{C})\) un signal on a
Les réseaux convolutifs sont construits pour traiter des problèmes de type traitement du signal sur des images. Un problème classique d'apprentissage est la classification. Imaginons qu'on est une image \(x\) et que l'on souhaite déterminer si l'image est un chat ou non. On souhaite construire
qui donne la probabilité qu'une image soit un chat ou non. Maintenant raisonnons au niveau du problème qu'on souhaite approcher. Si on applique de translations ou des rotations à l'image a priori le résultat doit rester inchanger notre problème est donc invariant pour les groupes de translation et rotation. Si maintenant on regarde un problème de segmentation ou l'on veut un pixel noir dans le chat et blanc en dehors. On cherche donc a construire une fonction du type
ici qu'on applique une translation ou rotation avant ou après la segmentation le résultat ne doit pas changer. On a donc un problème équivariant pour les groupes de translation et rotation. On illustre cela sur l'image suivante
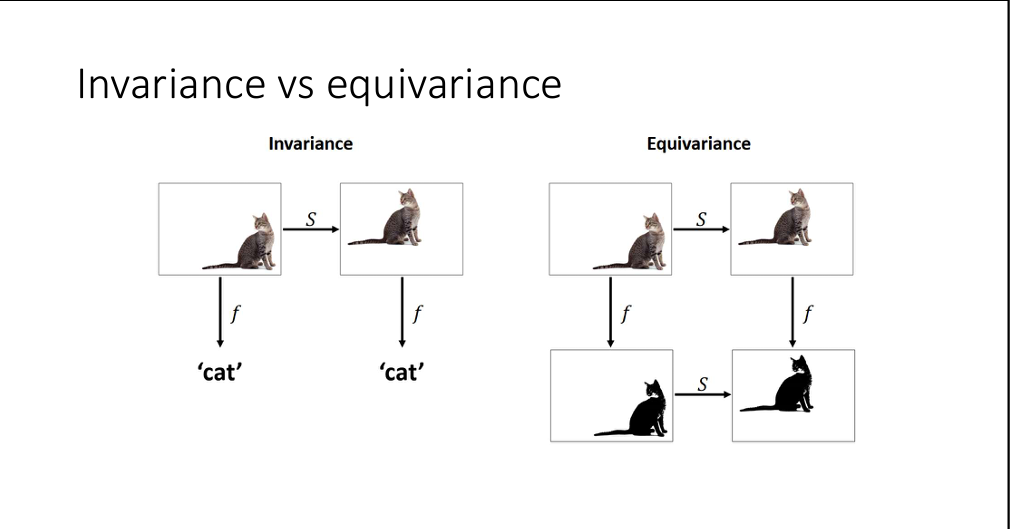
Puisqu'on sait ce que la fonction recherchée admet ce genre de symétrie si on en tient compte, cela permet de réduire l'espace des fonctions cibles. Afin que cette réduction soit effective on va encoder un de ces a priori géométriques dans la structure du réseau. En pratique le plus facile est l'invariance par translation.
On va considérer le cas 1D. Soir une grille \(\Omega\in \mathbb{Z}\) et un signal sur cette grille \(\bs{x} \in\mathbb{R}^{n}\text{.}\) Une couche de réseaux de neurones se décompose en une partie linéaire et une partie nonlinéaire. L'objectif est de déterminer une couche equivariant. La translation d'un pixel vers la droite est définie par
Si on veut appliquer une translation de \(k\) pixel il suffit de composer cette matrice \(k\) fois. On nomme l'opérateur \(S^k\text{.}\)
Proposition 5.31.
Soit la couche \(L(\bs{x})=\sigma (A \bs{x} + \bs{b})\) avec une matrice circulante de la forme
avec \(\bs{b}=0\text{.}\) Cette couche est équivariante par translation et donc satisfait
Preuve.
-
Partie linéaire:
La matrice de translation \(S^k\) est aussi une matrice circulante. Hors le produit de matrices circulantes est une matrice circulante et le produit est commutatif. Par conséquent
\begin{equation*} A S^k \bs{x} = S^k A\bs{x} \end{equation*} -
Partie non-linéaire:
La non-linéarité est appliquée localement a chaque composante du vecteur on voit donc qu'appliquer la non-linéarité puis translaté les composantes ou faire l'inverse donne un résultat identique.
On compose les deux parties de la couche maintenant et on a:
ce qui conclut la preuve.
On voit donc que pour obtenir une couche équivariante il suffit de choisir une matrice circulante. Pourquoi appelle-t-on nos réseaux des réseaux convolutifs ? Parce que les matrices sont circulantes sont les matrices des convolution discretes. Par conséquent lorsqu'on applique la partie linéaire de notre couche on est entrain d'appliquer une convolution discrète avec un filtre qu'on doit appendre. L'application de filtre par un produit de convolution est finalement assez naturelle pour introduire un traitement sur un signal.
En construction symétrie rotation et les deux ensembles
Subsubsection 5.2.1.2 Stabilité aux déformations et séparation d'échelle
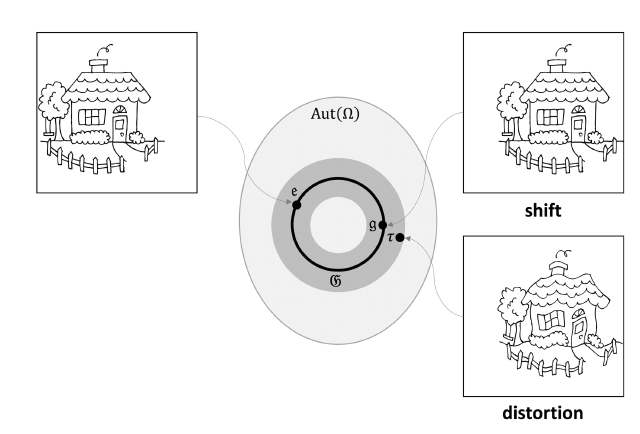
Avec ce choix, on vient de faire un premier choix pour définir notre couche de convolution. Cependant ce n'est pas suffisant. L'idée est d'introduire un second a priori dans la structure de notre réseau. Ce second a priori est appelé stabilité aux petites déformations. L'idée est simple, si on applique une petite déformation au signal d'entrée on s'attend à ce que la sortie soit peu ou pas modifiée. Si on reprend l'exemple de l'image du chat, une légère dilatation implique un léger changement sur le résultat d'une segmentation par exemple. Pour formaliser cela on introduit le groupe des automorphismes sur \(\Omega\) noté \(Aut(\Omega)\text{.}\) Soit \(\tau\) un élément \(Aut(\Omega)\text{.}\) On note une mesure de \(\tau\text{,}\) \(c(\tau)\) qui est nulle pour les éléments de groupe de translation. On peut choisir par exemple: \(\operatorname{sup}_{u\in \Omega}\parallel \nabla \tau(u)\parallel_2^2\text{.}\) Soit un signal \(x\in L(\Omega,\mathbb{R})\) une transformation sur les signaux \(f\text{.}\) Cette transformation est dite stable aux déformations si avec \(\rho(\tau)x=x(\tau^{-1}u)\text{.}\)
Définition 5.32. Stabilité aux déformations.
avec \(\omega\) la fréquence. Imaginons qu'on est un signal tel que
On a donc lorsqu'on applique la petite déformation:
donc
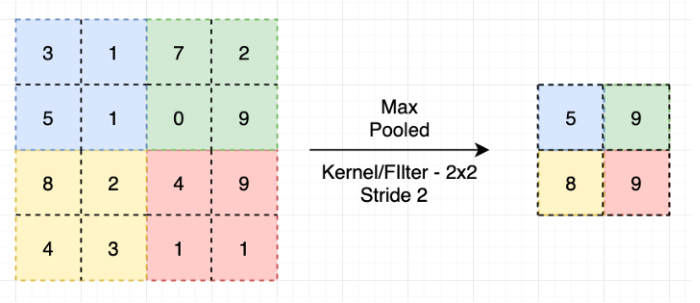
On a donc en plus de la dilatation des deux gaussiennes une translation du centre de taille \(\epsilon \omega_0\text{.}\) Si la fréquence \(\omega_0\) la translation du centre peut devenir importante et donc les supports des gaussiennes d'origines et de celles translatées deviennent disjoints. Dans ce cas la distance \(\mid f(x)-f(g\cdot \tau)\mid\) pourra être grande pour toute une gamme de valeur de \(\epsilon\text{.}\) On voit donc que les opérations agissant sur le spectre entier du signal comme le module sont instable pour les hautes fréquences. On peut en déduire qu'utiliser des convolutions appliquant des filtres globaux peuvent être assez instable. On ne détaillera pas, mais a l'inverse introduire des transformations locales (comme ce qu'on fait avec des ondelettes) est stable par rapport aux petites déformations. Afin d'obtenir de la stabilité par rapport aux petites déformations on choisit d'appliquer des filtres (noyaux) localisés en espace dans nos couches convolutives. On obtient donc des matrices de poids creuses avec un nombre faible de diagonales non nulles. Le stencil du noyau de convolution dans chaque direction (équivalent aux nombres de diagonales non nulles) se nomme taille des noyaux. Soit une entrée composée de plusieurs canaux (signaux) \(x=(x_1,...,x_m)\) avec \(x_i\) en dimension \(d\) (1,2 ou 3) avec \(n\) données par dimension. Une couche convolutive applique \(k\) filtres de convolution (donc multiplie chaque signal par \(k\) matrices circulantes) et on obtient en sorti \(k\) signaux. Cela revient d'entrée de taille \(m \times n^d\) et une sortie de taille \(k\times n^d\text{:}\) pour \(0\le i\le k\text{.}\) Soit un signal \(x\) en dimension \(d\) avec \(n\) données par dimension. L'opérateur de pooling est un opérateur de \(\mathbb{R}^{n^d}\) vers \(\mathbb{R}^{(\frac{n}{k})^d}\) ou \(k \times d\) pixel sont transformés en \(1\) pixel. Si on prend la moyenne on parle pooling moyen local. Si on prend le maximum on parle pooling maximal local.Filtres locaux en espaces.
Définition 5.34. Couche de convolution.

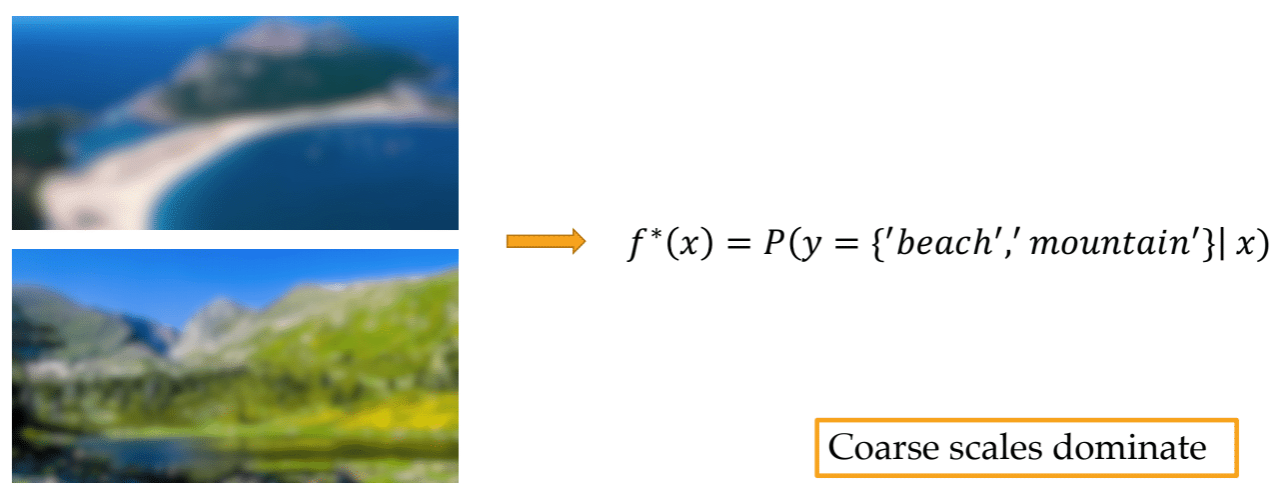

Définition 5.37. Couche de "pooling".
Subsection 5.2.2 Architectures de réseau convolutifs
Dans les réseaux convolutifs on applique en général plusieurs filtres convolutifs sur chaque signal (on parle channel). En enchaînant des couches convolutifs et de pooling on obtient à la fin une série de signaux de petite taille. En classification on cherche à obtenir à la fin un nombre unique dans \([0,1]\text{.}\) Pour convertir nos signaux on applique une couche d'aplatissement du signal appelé flatten et ensuite on applique un réseau totalement connecté. 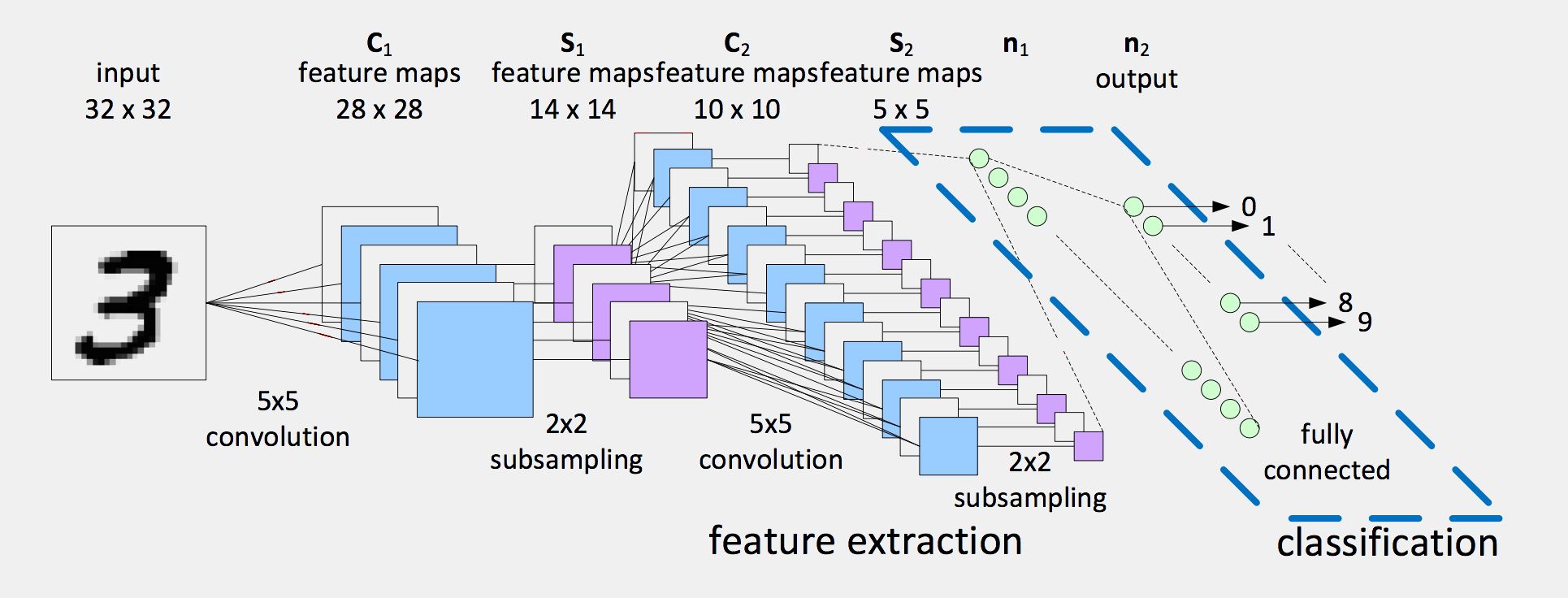
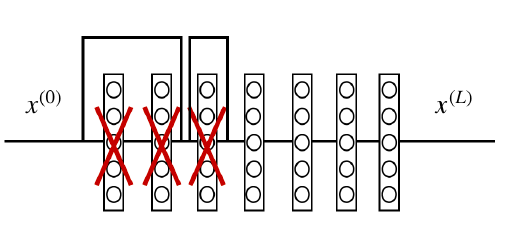
Définition 5.41. Couche et bloc résiduels.
On appelle une couche de neurones résiduelle une fonction \(L:\bs{x}\in \mathbb{R}^{d_i} \rightarrow \bs{y}\in\mathbb{R}^{d_{i+1}}\) définie par
On appelle un bloc (séries de couches répétées) residuel un bloc de la forme:
avec \(L_{i,i+1}\) des couches.
On voit que les réseaux ResNet on ajoute l'identité ( on parle de "shortcut" aussi) avant d'appliquer la non-linéarité à une couche ou a un bloc. Évidemment la présence de cette identité permet de stabiliser le gradient. Une des propriétés de cette approche est de changer la structure des fonctions approximables lorsqu'on augmente le nombre de couches. 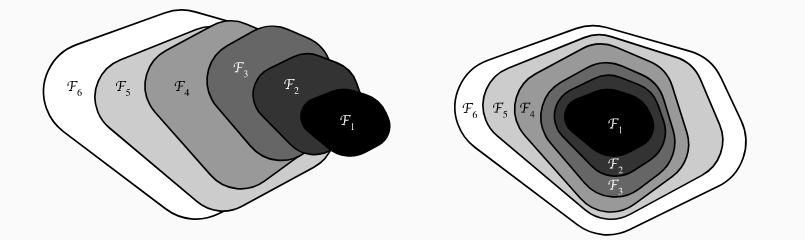

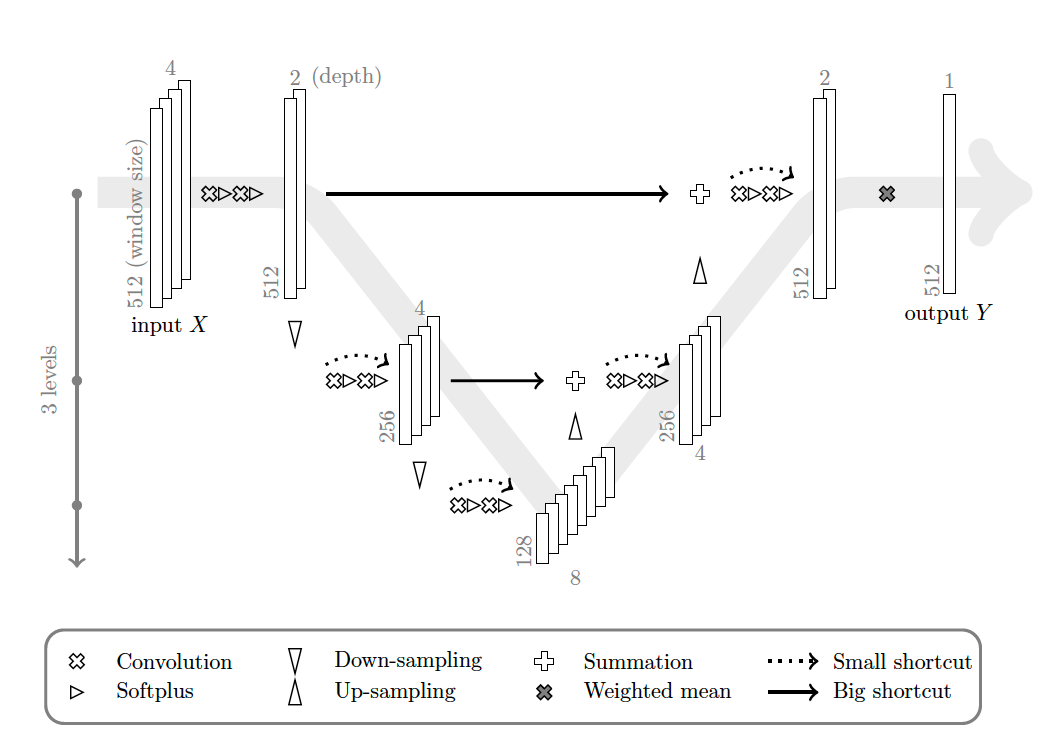
Subsection 5.2.3 Comparaison avec les réseaux totalement connecté
On a expliqué précédemment que les réseaux convolutifs encodaient dans leurs structures des apriori sur les problèmes de traitement du signal. Ces apriori vont permettent d'obtenir des meilleurs réesultats avec des réseaux totalement connectés. Pour montrer cela on va introduire un cas test simple.
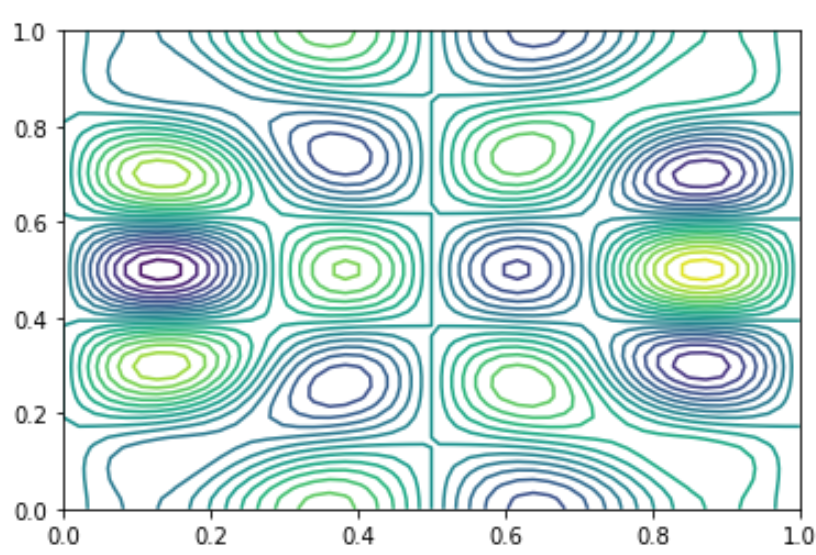
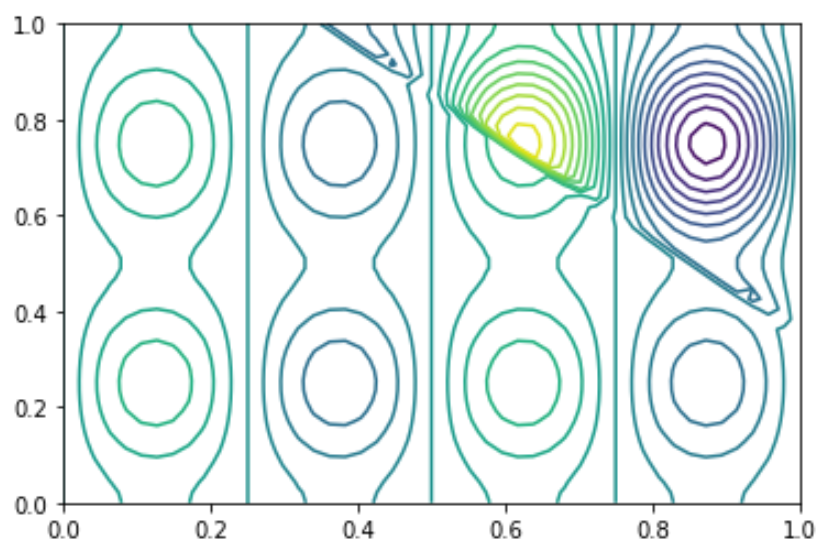
On génère aléatoirement des sinus de fréquentes différentes et on ajoute aléatoirement des discontinuités dans les fonctions obtenues. On obtient donc des images de sinus, avec dans certains cas des discontinuités. On se propose, de résoudre un problème de classification qui detecte dans quel image il existe des discontiuités. On donne un exemple sur la figure suivante Figure 5.45.