Section 6.3 Modèles génératifs a variables latentes et VAE
Ici on va introduire des modèles génératifs qui sont basées sur des variables latentes. Cela veut dire qu'on va utiliser des variables cachés (souvent en basse dimension) pour générer de nouvelles données.
Subsection 6.3.1 Modèles génératifs a variable latente
Les modèles génératifs forment un champ de recherche extrêmement actif en IA. Il s'agit de modèle dont le rôle est d'approcher des lois de probabilités \(p(x)\) en grande dimension. Par exemple on souhaite approcher la loi de probabilité des images de chat ou des protéines avec une certaine structure et on espère en échantillonnant la loi obtenue on obtienne de nouvelles images ou de nouvelles molécules. Il s'agit d'un problème différent de la réduction de dimension. Cependant certains de ses modèles utilisent une représentation en basse dimension et peuvent être utilisés pour compresser des EDP ou des processus stochastiques. On en profite donc pour introduire cette thématique.
On se donne un échantillon \((x_1,...x_n)\) ou chaque exemple appartient à \(\mathbb{R}^d\text{.}\) On suppose que ces échantillons suivent une loi de probabilité de densité \(p(x)\text{.}\) Comme précédemment on peut supposer qu'il est possible de représenter ces données en basses dimension. On peut réécrire cela comme l'hypothèse suivante. On dit qu'une loi de probabilité peut s'écrire comme un problème à variable latente si Soit \((x_1,...x_n)\) un échantillon i.d.d de densité de probabilité \(p(x)\text{.}\) Soit \(p(z)\) une loi de probabilité connue a priori. On se donne le modèle Un problème de réduction de dimension revient à résoudre le problème de maximum de vraisemblance On se ramène souvent au problème de log vraisemblance
Définition 6.8.
Définition 6.9.
En pratique, si on suppose que la distribution \(p(x)\) n'est pas triviale, on peut naturellement supposer qu'il faut que la transformation de \(z\) vers \(x\) le soit aussi et donc que \(p_{\theta}(x\mid z)\) ne sont pas un modèle trop simpliste. Si on part de cette hypothèse on se retrouve facilement dans la situation ou le problème est dit intractable, c'est-à-dire le cas ou ne sait pas calculer analytiquement:
TOO exemple. Dans la suite on va montrer comment on peut résoudre ce problème par des méthodes approchées. On va ensuite construire un premier modèle profond probabiliste.
Subsubsection 6.3.1.1 Inférence variationnelle
L'inférence variationnelle est une approche permettant des modèles probabilistes à variable latente lorsque certaines intégrales sont intractables. Il existe une approche concurrente appelée Markov Chain Monte Carlo. Ici on se donne les hypothèses suivantes:
La Distribution à priori est connue
la Distribution d'échantillonnage \(p_{\theta}(x\mid z)\) suit une certaine loi de paramètres inconnus.
Dans ce cas générale l'intégrale (6.3) est toujours incalculable. On utilise la régle de Bayses qui nous dit que
On voit si on construit \(p(z\mid x)\) on pourra estimer notre loi de probabilité \(p(x)\) et calculer le problème de maximum de log vraisemblance. Cependant on n'a pas d'information sur \(p(z\mid x)\) et même en connaissant les lois a priori et d'échantillon on ne peut pas déduire cette loi a posteriori. L'idée de l'approche variationnelle est de construire une approximation paramétrique de \(p(z\mid x)\) que l'ont note \(q_{\phi}(z\mid x)\text{.}\) Pour cela il faut se donner un critère de construction sur \(q_{\phi}(z\mid x)\text{.}\) On avait introduit précédemment la divergence de Kullback-Leibler qui définie une pseudo distance entre des distributions de probabilité (pas de symétrie) et qui correspond à la limite pour un grand nombre d'échantillons de la log-vraisemblance. Pour construire l'approximation \(q_{\phi}(z\mid x)\) on souhaite donc minimiser sur les échantillons
À l'aide de ce critère, on peut donc obtenir un problème à résoudre qui définit notre modèle à variables latentes. Soit \((x_1,...x_n)\) un échantillon i.d.d de densité de probabilité \(p(x)\text{.}\) Soit \(p(z)\) un loi de probabilité connu a priori. Soit \(p_{\theta}(x\mid z)\) de loi connue et de paramètres inconnus. Le problème de maximisation de la log vraisemblance précédente peut être approché par le problème. Résoudre le problème de minimisation
Proposition 6.10.
Lemme 6.11.
Résoudre le problème de minimisation
est équivalent au problème de minimisation
avec \(Loss_{ELBO}\) aussi égale à
Preuve.
On commence par utiliser la définition de la divergence Kullback-Leibler
Il suffit de réarranger la gauche et la droite pour conclure la preuve. Pour obtenir la réécriture de la fonction de coût il suffit d'utiliser les propriétés du log.
On parle de ELBO ou borne inférieure de la vraisemblance, car l'inverse de la fonction coût (ou loss) est un minorant de la fonction de vraisemblance. Ici on voit que notre loi a été réécrite sans intégrale a calculer et dépend uniquement de loi paramètres ou de loi connue (ici \(p(z)\)) qu'on sait échantillonner. On a donc une nouvelle fonction coût à minimiser qu'on sait calculer en pratique. Maintenant on va utiliser ce résultat afin de construire une méthode de réduction de dimension.
Subsubsection 6.3.1.2 Auto-Encoder variationnel
L'auto-encodeur variationnel (VAE) est un modèle probabiliste à variables latentes. On chercher ici a construire des loi
qui permettent de compresser et décompresser de façon probabiliste des données. Comme précédemment on se donne ici un a priori \(p(z)\) et on cherche a maximiser la vraisemblance sur un échantillon \((x_1,...,x_n)\text{.}\) On retrouve le processus sur la figure Figure 6.12. 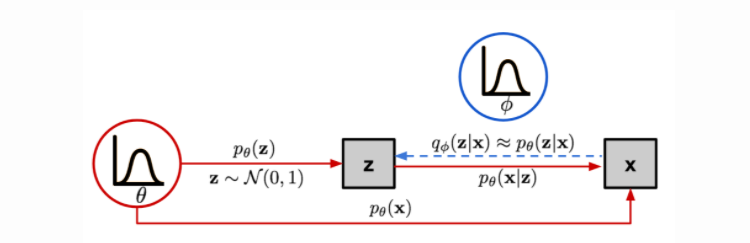
Distribution à priori: \(p(z)=\mathcal{N}(0,I_d)\text{,}\)
Distribution d'échantillonnage: \(p_{\theta}(x\mid z)=\mathcal{N}(\mu_{\theta}(z),c_{\theta}(z) I_d)\text{,}\)
avec \(\mu_{\theta}(z)\) et \(c_{\theta}(z)\) un réseau de neurones potentiellement complexe. C'est ce réseau de neurones qui rend l'intégrale
est intractable. Pour cette raison utilise l'approche variationnelle précédente et pour cela on décide d'utiliser:
avec \(\mu_{\phi}(x)\) et \(c_{\phi}(x)\) un autre réseau de neurones. Pour effectuer l'apprentissage de ces deux réseaux de neurones on va minimiser le problème (6.5). En général on fait cela avec des méthodes de gradients (comme introduit précédemment) et il faut donc être capable de calculer le gradient de cette fonction coût par rapport à \(\theta,\phi\text{.}\) Afin d'effectuer un apprentissage par des méthodes de gradient stochastique avec de la rétropropagation (comme habituellement pour les réseaux de neurones) on souhaite calculer les gradients par rapport aux paramètres. Commençons par le gradient pas rapport à \(\theta\text{:}\)
On peut permuter le gradient et la divergence facilement, car les variables latentes \(z\) sont générées indépendamment de \(\theta\) et donc l'espérance aussi. Le terme en divergence ne dépend pas non plus de \(\theta\) donc on obtient facilement le résultat. On a donc l'espérance d'un gradient et cela peut se traiter facilement avec une méthode de Monte-Carlo comme on a pu le voir précédemment:
avec \(z_i\sim q_{\phi}(z_i\mid x_i)\text{.}\) Dans le cas gaussien (cas du VAE) ou \(\theta\) intervient dans la variance et l'espérance on peut calculer explicitement le gradient par rapport à \(\theta\) de \(\operatorname{log} p_{\theta}(x\mid z)\) comme on l'a vu dans les rappels de maximum de vraisemblance. Maintenant on considère le gradient par rapport au second paramètre:
La difficulté ici vient du fait qu'on calcule le gradient d'une espérance avec la loi associée qui dépend elle-même des paramètres. On a donc
et donc on ne peut pas traiter ce terme avec le gradient stochastique habituel. Il existe une méthode pour réécrire ce gradient appelé la méthode Reinforce à qui on applique une approximation de Monte Carlo. Cependant cet estimateur du gradient d'origine admet une forte variance. Dans le papier d'origine sur les VAE il propose une autre approche permettant d'effectuer la rétropropagation et d'obtenir un meilleur estimateur. Pour permettre cette rétropropagation du gradient il est proposé de réécrire la génération de \(z\) sous la forme suivante:
avec \(\epsilon\) une variable aléatoire. Dans ce cas la fonction qui dépend des paramètres \(\phi\) par rapport auxquels on veut calculer le gradient devient déterministe (avant c'était un processus aléatoire) et l'aléa est introduit comme une entrée de la fonction. Cela revient à écrire:
ou on peut facilement rentrer \(\nabla_{\phi}\) dans l'espérance comme précédemment et donc utiliser ensuite une approche Monte-Carlo pour le calculer. Maintenant il faut déterminer la fonction \(T_{\phi}\text{.}\) On sait que
Grâce aux propriétés des lois gaussiennes on a que
avec \(\epsilon\sim \mathcal{N}(0,I_d)\) et \(\odot\) le produit élement par élément. Avec cette stratégie on se retrouve avec la possibilité de calculer les deux gradients nécessaires à l'apprentissage.
Pour finir, en utilisant nos hypothèses gaussiennes (qui peuvent être changées) on peut réécrire la fonction coût de notre VAE. Soit \(p(z)=\mathcal{N}(0,I_d)\text{,}\) \(p_{\theta}(x\mid z)=\mathcal{N}(\mu^d_{\theta}(z),c^d_{\theta}(z) I_d)\) et \(q_{\phi}(z\mid x)=\mathcal{N}(\mu^e_{\theta}(x),c^e_{\theta}(x) I_d)\text{.}\) Dans e cas la fonction de coût se réécrit avec \(K\) la dimension de l'espace réduit.
Proposition 6.13.
Preuve.
Subsubsection 6.3.1.3 \(\beta\)-VAE
Le premier variant est l'algorithme \(\beta\)-VAE. Son objectif est d'obtenir des représentations réduites dites désenchevetrées. Cela revient à dire que chaque variable réduite est fortement sensible a une caractéristique des données \(x\) et assez invariantes aux autres caractéristiques. Cela permet d’obtenir de meilleur résultat de généralisation. Ce peut s'interpréter comme une notion proche de l'orthogonalité pour les méthodes de types PCA.\\ Pour cela l'idée est d'ajouter une contrainte du type
En contraignant la distance entre notre loi a posteriori et l'a priori gaussien isotrope on contraint une certaine indépendance dans les variables réduites générer par \(q_{\phi}(z\mid x)\text{.}\) En effet une loi gaussienne multivariée isotrope (matrice de covariance diagonale) revient à dire dire que chaque dimension de la gaussienne (ici les variables latentes \(z_i\)) sont independantes. On force donc ici une certaine indépendance des variables latentes entre elles. On va maintenant regarder comment cela se traduit en pratique. On rappelle la fonction de coût du VAE:
Afin de trainter la contrainte, on introduit un Lagrangien de multiplicateur de Lagrange \(\beta\) qui satisfait les conditions de Karush-Kuhn-Tucker. Notre problème de minimisation revient donc à minimiser:
ce qui est égal à
Puisque \(\beta\delta \gt 0\text{,}\) minimiser l'équation précédente revient juste à minimiser
Cette fonction de coût est quasiment identique à celle utilisée pour le VAE et identique pour \(\beta=1\text{.}\) Il est naturelle de prendre \(\beta \gt 1\) pour augmenter l'indépendance des variables réduites.