Réseaux de neurones physiquement informés

Section 12.4 Réseaux de neurones physiquement informés

Les PINN's pour "physic informed neural network" ont été introduit en 2017 dans (...) afin de résoudre une EDP a l'aide de réseaux de neurones. L'idée central revient a résoudre une EDP sous forme d'un problème d'optimisation.

Subsection 12.4.1 Introduction aux réseaux physiquement informés

On va commencer par illustrer la méthode le cas générale d'une EDP de type:

\begin{equation} \left\{\begin{array}{l} \partial_t \bs{U}=\mathcal{N}(\bs{U},\partial_x \bs{U}, \partial_{xx} \bs{U},\boldsymbol{\beta}) \\ \bs{U}_h(t,x)=g(x),\quad \forall x \in \partial \Omega\\ \bs{U}(0,x)=\bs{U}_0(x,\boldsymbol{\alpha}) \end{array}\right.\tag{12.1} \end{equation}

avec \(\boldsymbol{\mu}=(\boldsymbol{\alpha},\boldsymbol{\beta})\) un ensemble de paramètres. Notre modèle de Burgers rentre évidemment dans ce cadre général.

On suppose que l'on a une approximation de notre solution \(\mathbf{U}(t,x)\) que l'ont notera \(\mathbf{U}_h(t,x)\text{.}\) On note \(\mathcal{F}\) l'espace des fonctions admissible que l'on considère et on suppose \(\mathcal{F}\subset C^k(\Omega \times [0,T])\) (avec \(\Omega\) le domaine). La première idée des PINNs vient du constat que par construction les réseaux de neurones sont des fonctions régulières plusieurs fois dérivables par rapport à leurs poids et leurs entrées. Par conséquent les réseaux de neurones dont les dérivées sont facilement évaluables par différentiation automatique forment des candidats naturels d'approximation d'EDP. Un PINNs est un réseau de neurones qui prend comme entrée \((t,x)\text{,}\) on le notera ici \(\mathbf{U}_{\theta}(t,x)\text{.}\) Une fois ce réseau défini résoudre l'EDP peut se réécrire sous la formule du problème variationnel suivant

\begin{equation} \operatorname{min}_{\theta} J_r(\theta)+J_b(\theta)+J_i(\theta)+J_{data}(\theta)\tag{12.2} \end{equation}

avec

\begin{equation} J_r(\theta)=\int_0^T\int_{\Omega}\parallel \partial_t\mathbf{U}_{\theta}(t,x)-\mathcal{L}(\mathbf{U}_{\theta},\partial_x \mathbf{U}_{\theta}, \partial_{xx} \mathbf{U}_{\theta},\boldsymbol{\mu})(t,x)\parallel_2^2 dxdt \tag{12.3} \end{equation}

\begin{equation} J_b(\theta)=\int_0^T \int_{\partial \Omega} \parallel \mathbf{U}_{\theta}(t,x)-g(x)\parallel_2^2 dxdt,\quad J_i(\theta)=\int_{\Omega} \parallel \mathbf{U}_{\theta}(0,x)-\mathbf{U}_{0}(x)\parallel_2^2 dx\tag{12.4} \end{equation}

Ce problème de minimisation revient a minimiser le résidu lorsqu'on incorpore notre solution approchée dans l'EDP avec condition initiale et limite. Si on est capable de calculer l'intégrale précédente on peut résoudre le problème de minimisation (phase d'apprentissage) par une méthode de gradient (par rapport à \(\theta\)). Le second ingrédient dans la méthode PINNS porte justement sur le calcul de l'intégrale. L'idée la plus naturelle est d'estimer l'intégrale à l'aide d'une méthode Monte-Carlo. On va donc se donner un certain nombre de points dit de "collocation" (a priori choisie aléatoirement) et approcher l'intégrale avec. On se donne par exemple les points:

\begin{equation*} (t_1,x_1,.....t_N,x_N). \end{equation*}

Avec ces points on peut par exemple approcher l'intégrale (12.2) de la façon suivante

\begin{equation*} \frac{1}{N}\sum_{i=1}^N \parallel \partial_t\mathbf{U}_{\theta}(t_i,x_i)-\mathcal{L}(\mathbf{U}_{\theta},\partial_x \mathbf{U}_{\theta}, \partial_{xx} \mathbf{U}_{\theta},\boldsymbol{\beta})(t_i,x_i)\parallel_2^2 \end{equation*}

La convergence de la méthode de Monte Carlo étant lente on souhaite l'accélérer. Une première possilibité est de choisir les points de façon plus astucieuse avec des approches type échantillonnage préférentiel. On y reviendra plus tard. Même si l'intégrale est bien approchée par une méthode de Monte-Carlo, le processus d'optimisation peut être aussi assez lent notamment parcequ'on ne minimise pas une fonction de coût classique \(\parallel f_{\theta}(x_i)-y_i\parallel\text{,}\) mais une version implicite \(\parallel g(f_{\theta}(x_i))-z_i\parallel\) (avec \(z_i=0\) dans notre cas). Pour aider l'apprentissage, on peut se donner un certain nombre de points ou on connaît exactement la solution. Cela revient à avoir

\begin{equation*} (t_1,x_1,\mathbf{U}_1,.....t_N,x_N,\mathbf{U}_N) \end{equation*}

Ces exemples peuvent venir d'un autre solveur dans ce cas le PINNs peut être utile pour créer une interpolation efficace entre des données issues d'un solveur. On peut citer comme applications la super résolution (ref). Cela peut aussi être de vrai données avec lequel on va enrichir ou corriger le modèle. Dans ce cas on peut minimiser l'erreur suivante

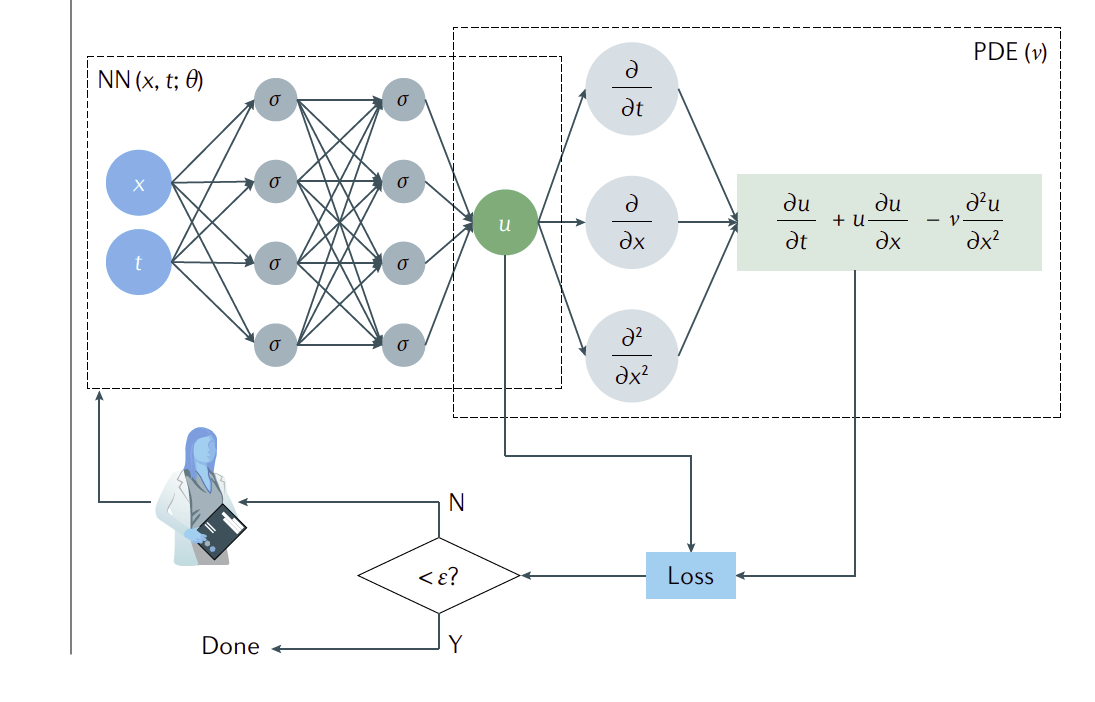
\begin{equation*} \sum_{i=1}^{N}\parallel \mathbf{U}_h(t_i,x_i)-\mathbf{U}_i\parallel_2^2 \end{equation*}

Figure 12.1. Fonctionnement d'un réseau PINNs.

Une fois tous ces ingrédients réunis cela nous permet de construire une fonction de coût globale pour les PINNS.

Définition 12.2. Fonction coût PINNS.

la fonction de coût des PINNS s'écrit

\begin{equation*} \mathcal{L}_{PINNs}(\theta)=c_{1}\mathcal{L}_{mc,r}(\theta) +c_{2}\mathcal{L}_{mc,b}(\theta)+ c_{3}\mathcal{L}_{mc,i}(\theta) +c_{4}\mathcal{L}_s(\theta) \end{equation*}

avec

\begin{equation*} \mathcal{L}_{mc,r}(\theta) =\sum_{i=1}^{N_r} \parallel \partial_t \mathbf{U}_h(t_i^r,x_i^r)-\mathcal{L}(\mathbf{U},\partial_x \mathbf{U}, \partial_{xx} \mathbf{U},\beta) (t_i^r,x_i^r)\parallel_2^2 \end{equation*}

la fonction coût du résidu et \((t_1^r,x_1^r,...,t_i^r,x_i^r,...)\) les points utilisés pour évaluer le résidu, avec

\begin{equation*} \mathcal{L}_{mc,b}(\theta) =\sum_{i=1}^{N_b}\parallel \mathbf{U}_h(t_i^d,0)-\mathbf{U}_l\parallel_2^2 + \sum_{i=1}^{N_b}\parallel \mathbf{U}_h(t_i^d,L)-\mathbf{U}_r\parallel_2^2 \end{equation*}

la fonction coût du résidu et \((t_1^b,...,t_i^b,...)\) les points utilisés pour évaluer la condition limite,

\begin{equation*} \mathcal{L}_{mc,i}(\theta) =\sum_{i=1}^{N_i}\parallel \mathbf{U}_h(0,x_i^i)-\mathbf{U}_0(x_i^i,\alpha)\parallel_2^2 \end{equation*}

la fonction coût du résidu et \((x_1^i,...,x_i^i,..)\) les points utilisés pour évaluer la condition initiale et avec

\begin{equation*} \mathcal{L}_s(\theta) =\sum_{i=1}^{N_d}\parallel \mathbf{U}_h(t_i^d,x_i^d)-\mathbf{U}_i\parallel_2^2 \end{equation*}

la fonction coût du résidu et \((t_1^s,x_1^s,..,t_i^s,x_i^s,...)\) les points utilisés pour évaluer les données.

Ici on voit que le choix des points de collocation sont séparés entre le bord, la condition limite, le résidu et l'apprentissage supervisé. Cela permet d'utiliser des lois d'échantillonnage différentes selon les intégrales et des nombres de points différents. Si on ne se séparait pas les calculs des fonctions de coût associées aux bords et à la condition initiale on risquerait de mal capturer les solutions aux bords et initiales. En effet en tirant aléatoirement les points dans le domaine sans séparer les bords on aurait eu probablement trop peu de points sur les frontières du domaine espace-temps. Pour les données intérieures et le résidu, on peut prendre les mêmes points ou des points différents. On voit aussi que de façon générale le poids entre les fonctions de coût restent à déterminer. Dans (ref sun2020surrogate) les auteurs de proposer une autre approche pour coder en dur les conditions initiales et aux limites. Cela permet notamment d'améliorer la précision des PINN's. Pour cela on définit

\begin{equation*} \hat{\mathbf{U}}_{\theta}(t,x)=\mathbf{U}_{par}(t,x)+\psi(t,x)\mathbf{U}_{\theta}(t,x) \end{equation*}

avec \(\psi(t,x)\) une fonction analytique régulière et \(\mathbf{U}_{par}(t,x)\) une fonction donnée qui n'est pas un réseau de neurones. On va définir la fonction particulière de la façon suivante:

\begin{equation*} \mathbf{U}_{par}(t,x)= \chi_{\left\{t=0\right\}}\mathbf{U}_0(x)+\chi_{\left\{x\in \partial \Omega \right\}}g(x) \end{equation*}

On qu'en prenant \(\psi(t,x)\) une solution régulière qui est nulle aux bords \(x\in \partial \Omega\) et \(t=0\) on va se retrouver dans un cas ou \(\hat{\mathbf{U}}_{\theta}(t,x)=\mathbf{U}_{par}(t,x)\) au bord du domaine espace-temps. Un choix simple de fonction \(\psi\) pourrait être \(\psi(t,x)=x(1-x)t\text{.}\) Dans cette condition on se retrouve avec une unique fonction de coût a minimiser:

\begin{equation} J_r(\theta)=\int_0^T\int_{\Omega}\parallel \partial_t\hat{\mathbf{U}}_{\theta}(t,x)- \mathcal{L}(\hat{\mathbf{U}}_{\theta},\partial_x \hat{\mathbf{U}}_{\theta}, \partial_{xx} \hat{\mathbf{U}}_{\theta},\boldsymbol{\beta})(t,x)\parallel_2^2 dxdt \tag{12.5} \end{equation}

La méthode PINNs admet deux avantages principaux par rapport aux méthodes numériques classiques: elles sont sans maillages et peu sensible à la dimension de l'EDP. Par contre leurs convergences semblent assez lentes. Pour converger, il faut à la fois un réseau assez puissant pour capturer la solution et un entraînement assez efficace mais il faut aussi approcher l'intégrale présente dans la fonction coût .

Subsubsection 12.4.1.1 Fonction d'activation

Contrairement aux applications en traitement du signal, la fonction d'activation la plus utilisée n'est pas la fonction RELU. En pratique il ne s'agit pas d'une fonction \(C^1/\text{.}\) En régularisant, on peut aisément la dériver par différentiation automatique, mais le réseau obtenu n'est pas assez régulier pour être dérivé deux fois (ce qui est nécessaire pour les termes homogènes à un Laplacien). La fonction d'activation utilisée dans le papier d'origine est la fonction Tangente hyperbolique qui est régulière et plusieurs fois dérivable. Dans [1.21] propose d'utiliser une approche introduite en traitement du signal. Il s'agit de faire dépendre les fonctions d'activation d'un paramètre qui va lui aussi être appris durant l'entraînement. Voici quelques exemples:

Relu adaptative: \(\sigma_a(x)=\operatorname{max}(0,a x)\)
Leaky Relu adaptative: \(\sigma_a(x)=\operatorname{max}(0,a x)-\nu \operatorname{max}(0,-a x)\)
Tangente hyperbolique adaptative: \(\sigma_a(x)=\frac{e^{ax}-e^{-ax}}{e^{ax}+e^{-ax}}\)
Sigmoide adaptative: \(\sigma_a(x)=\frac{1}{1+e^{-ax}}\)

Dans [1.21] il propose de fixer le paramètre \(a\) pour toutes les couches. Cela devient donc un hyper-paramètres qu'on optimise avec la même méthode de gradient que les poids du réseau.

Subsection 12.4.2 Etude de l'apprentissage des réseaux: l'approche NTK

L'approche dite NTK (pour Neural Tangent kernel) est une approche générale pour étudier la propriété de réseaux. Elle est très intéressante dans le cas des PINNs d'ou son introduction ici. On va donner un réseau de neurones \(f_{\theta}(x)\) avec \(x\in \mathbb{R}^d\text{.}\) On suppose que notre objectif est de minimiser la fonction de coût suivante:

\begin{equation*} \mathcal{J}(\theta)=\frac{1}{N}\sum_{i=1}^N l(f_{\theta}(x_i),y_i) \end{equation*}

avec \(l(f,y)\) la fonction de coût locale. Cette fonction coût est minimiser avec une méthode de gradient. Dans la sous section Subsection 3.2.5 on a introduit une vision continue des méthodes de gradient. En effet on peut supposer que les poids sont continument indexées par un paramètre \(t\) on a donc le réseau \(f_{\theta(t)}(x)\) et le cacul de ses poids est effectué en résolvant:

\begin{equation} \frac{d \theta(t)}{dt}=-\nabla \mathcal{J}(\theta(t))\tag{12.6} \end{equation}

et la descente est en pratique une discrétisation de cette ODE. L'enjeu de l'approche NTK est de mieux comprendre la dynamique du réseau lorsque les poids évoluent durant l'entrainement selon cette dynamique continue. On va repartir de (12.6). En utilisant la définition de la fonction cou on obtient:

\begin{equation} \frac{d \theta(t)}{dt}=-\frac{1}{N}\sum_{i=1}^N \nabla_{\theta(t)} l(f_{\theta(t)}(x_i),y_i)\tag{12.7} \end{equation}

ce qui donne

\begin{equation} \frac{d \theta(t)}{dt}=-\frac{1}{N}\sum_{i=1}^N \left(\nabla_{\theta(t)} f_{\theta(t)}(x_i) \right)\left( \nabla_{f} l(f,y_i) \right)\tag{12.8} \end{equation}

On utilise ensuite que

\begin{equation*} \frac{d f_{\theta(t)}(x)}{dt}= \left(\nabla_{\theta(t)} f_{\theta(t)}(x) \right)^T\frac{d \theta(t)}{dt} \end{equation*}

pour obtenir:

\begin{equation*} \frac{d f_{\theta(t)}(x)}{dt}=-\frac{1}{N}\sum_{i=1}^N \left(\nabla_{\theta(t)} f_{\theta(t)}(x) \right)^T\left(\nabla_{\theta(t)} f_{\theta(t)}(x_i) \right)\left( \nabla_{f} l(f,y_i) \right) \end{equation*}

Définition 12.3. Noyau NTK.

Soit un réseau \(f_{\theta(t)}\text{.}\) Le noyau NTK est définit par

\begin{equation*} k_{\theta}(x,y)= \left(\nabla_{\theta(t)} f_{\theta(t)}(x) \right)^T\left(\nabla_{\theta(t)} f_{\theta(t)}(y) \right) \end{equation*}

La dynamique d'apprentissage de \(f_{\theta(t)}\) dépend donc de ce noyau a travers:

\begin{equation*} \frac{d f_{\theta(t)}(x)}{dt}=-\frac{1}{N}\sum_{i=1}^N k_{\theta}(x,x_i) \left( \nabla_{f} l(f,y_i) \right) \end{equation*}

Si on caractérise ce noyau on caractérise la dynamiqur du réseau. Cependant ce noyau est un objet complexe qui évolue dans le temps et dont l'initialisation est aléatoire car les poids sont initialisés de façon aléatoire. On appelle ce noyau NTK car on peut considérer qu'il approche le réseau nonlinéaire par l'approximation linéaire tangeante du 1er ordre autour d'un paramètre fixé \(\theta_0\) par la formule:

\begin{equation*} f_{\theta(t)}(x)=f_{\theta_0}(x)+\left(\nabla_{\theta} f_{\theta_0}(x) \right) \theta(t) \end{equation*}

L'objectif est de comprendre la dynamique de ce noyau pour des réseaux avec initilisation aléatoire. Il est fréquement admis que les réseaux dit sur-paramétré donne de très bon résultats. Pour cette raison, il a été introduit dans plusieurs travaux les réseaux dit dans la \limite de sur-paramétrisation ce qui est équivalent, pour un réseau à \(L\) couches et \(n_1,....n_{L-1}\) le nombres de neurones a chaques couches, à la limite \(n_1,....n_{L-1}\) tends vers l'infini. Avant de continuer l'analyse on va introduire des résultats écrivant les réseaux profonds comme un processus Gaussien.

Subsubsection 12.4.2.1 Lien entre réseaux profonds et processus Gaussien

On va d'abord introduire des notations sur les réseaux de type MPC avant d'introduire le lien avec les processus Gaussien. Un réseau \(f_{\theta}(x)\) est défini par:

\begin{equation*} \begin{cases} g_0(x)=x\in \mathbb{R}^{in} \\ \tilde{g}_{l+1}(x_l)=\frac{1}{\sqrt{n_l}}\omega_l^t g_l(x) +\beta b_l \\ g_{l+1}(x)=\sigma(\tilde{g}_{l+1}) \end{cases} \end{equation*}

avec

\begin{equation*} f_{\theta}(x)=\tilde{g}_{L}(x) \in \mathbb{R}^{out} \end{equation*}

et \(\omega_l\in \mathcal{M}_{n_l,n_{l+1}}(\mathbb{R})\) la matrice des poids, \(b_l\) le biais, \(\beta \ge 0\) un paramètre qui indique la force du biais. La mise a l'échelle \(\frac{1}{\sqrt{n_l}}\) est important pour le passage à la limite. Les poids \(\theta_l=(\omega^l,b^l)\) sont générés par une loi \(\mathcal{N}(0,I_d)\text{.}\) Par conséquent les poids sont tous considérer comme independant car la covariance est l'identité.

Proposition 12.4.

Soit \(\theta_l=(\omega^l,b^l), \quad \forall 0\le l \le L\) sont générés par une loi \(\mathcal{N}(0,1)\text{.}\) La sortie d'un réseau à \(L\) couches, chaque sortie \(f_{\theta,i}(x)\) avec \(0\le i\le n_L\) dans la limite \((n_1,....n_{L-1})\rightarrow\infty \) associés a ces poids est générée par un processus gaussien centré de matrice de covariance \(\Sigma_{\infty}^L(x,y)\) définie de manière récursif par

\begin{equation*} \Sigma_{\infty}^1(x,y)=\langle x,y\rangle + \beta^2 \end{equation*}

\begin{equation*} \Sigma_{\infty}^{l+1}(x,y)=\mathbb{E}_{(u,v)\sim \mathcal{N}(0,\lambda_l)} [\sigma(u)\sigma(v)]+\beta^2 \end{equation*}

avec

\begin{equation*} \lambda_l(x,y)=\begin{pmatrix} \Sigma_{\infty}^l(x,x) \amp \Sigma_{\infty}^l(x,y)\\ \Sigma_{\infty}^l(y,x) \amp \Sigma_{\infty}^l(y,y) \end{pmatrix} \end{equation*}

Preuve.

On va faire la desmontration par récurrence sur la valeur \(L\text{.}\) On suppose qu'il que la dernière couche utilise une fonction d'activation linéaire.

montrons que la proposition est vrai pour \(L=1\text{:}\)

Dans ce cas on a:

\begin{equation*} g_{1}(x)=\frac{1}{\sqrt{n_0}}\omega^{0,t} g^0+\beta b^0 \end{equation*}

avec \(g_0(x)=x\) car la fonction d'activation est linéaire. Ceci est équivalent à

\begin{equation*} g_{1}^i(x)=\frac{1}{\sqrt{n_0}}\sum_{j=1}^{n_1}\omega_{ij}^0 g_j^0+\beta b_i^0 \end{equation*}

Puisque les poids et biais sont indépendant et identiquement distribués et que \(g_{1}^i(x)\) est une combinaison linéaire de \(\omega_{ij}^0,b_i^0\) alors par le théorème central limite nous dit que \(g_1^i(x)\) suit une loi normale. En appliquant des corollaire du théorème central limite on voit \((g_1^i(x_1),...,g_1^i(x_j),...g_1^i(x_N))\) suit une loi Gaussienne multivariée. Ceci étant vrai pour tout \((x_1,....,x_N)\) on voit que \(g_1(x) =\mathcal{GP}(\mu_1,\Sigma_1)\) par définition d'un processus Gaussien avec la moyenne et la variance indépendant de \(i\text{.}\) On commence par estimer la moyenne.

\begin{equation*} \mu_1=\mathbb{E}[g_1^i(x)]= \frac{1}{\sqrt{n_0}}\sum_{k=1}^{n_1}\mathbb{E}[\omega_{ik}^0] g_k^0+\beta \mathbb{E}[b_k^0] \end{equation*}

Ensuite on passe à la matrice de covariance:

\begin{align*} \Sigma_1(x,x^{'}) \amp =\mathbb{E}\left[g_1^i(x)g_1^j(x^{'})\right] \\ \Sigma_1(x,x^{'}) \amp =\mathbb{E}\left[ \left(\frac{1}{\sqrt{n_0}}\sum_{k=1}^{n_1}\omega_{ik}^0 g_k^0+\beta b_i^0\right) \left(\frac{1}{\sqrt{n_0}}\sum_{k=1}^{n_1}\omega_{0,jk} g_0^k+\beta b_j^0\right)\right] \\ \Sigma_1(x,x^{'}) \amp =\frac{1}{n_0}\mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^0 x_k\right) \left(\sum_{k=1}^{n_1}\omega_{jk}^0 x_k^{'}\right)\right]\\ \amp + 2 \frac{\beta}{\sqrt{n_0}}\mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^0 x_k\right)b_{i}^0 +\left(\sum_{k=1}^{n_1}\omega_{jk}^0 x_k\right)b_{j}^0 \right] +\beta^2\mathbb{E}\left[b_{i}^0 b_j^0\right] \end{align*}

Puisque que \(b_{i}^0 \sim \mathcal{N}(0,1)\) on a \(\mathbb{E}[b_{i}^0 b_j^0]=\delta_{ij}\text{.}\) Puisque \(\omega_{ij}^0\) et \(b_i^0\) dont indépendant alors:

\begin{equation*} \mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^0 x_k\right)b_{i}^0 +\left(\sum_{k=1}^{n_1}\omega_{jk}^0 x_k\right)b_{j}^0 \right]= \left(\sum_{k=1}^{n_1}\mathbb{E}[\omega_{ik}^0] x_k\right)\mathbb{E}[b_{i}^0] +\left(\sum_{k=1}^{n_1}\mathbb{E}[\omega_{jk}^0] x_k\right)\mathbb{E}[b_{j}^0] =0 \end{equation*}

pusiqu'on a choisit des poids et biais centrés. Eb développnant les calcul on obtient

\begin{equation*} \mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^0 x_k\right) \left(\sum_{k=1}^{n_1}\omega_{jk}^0 x_k^{'}\right)\right]= \langle x,x^{'}\rangle \delta_{ij} \end{equation*}

puisque \(\omega^0 \sim \mathcal{N}(0,1)\) cela permet de conclure la première partie de la preuve. Cela nous montre que \(g_i(x)\) et \(g_j(x)\) sont indépendants en plus d'être identiquement distribués.
On demontre la proposition pour \(L=l+1\) sachant qu'elel est vrai pour \(L=l\text{:}\)

Pour la récurrence on suppose donc que \(\tilde{g}_l^i(x)\sim \mathcal{GP}(0,\Sigma_l)\) et \(\tilde{g}_l^i\text{,}\) \(\tilde{g}_l^j\) sont indpéndants pour \(i\neq j\text{.}\) On va étudier \(\tilde{g}_l^i(x)\text{.}\) Puisque les poids et biais sont indépendant et identiquement distribués et que \(\tilde{g}_{l+1}^i(x)\) est une combinaison linéaire de \(\omega_{ij}^l,b_i^l\) et \(\sigma(\tilde{g}_{l}^i(x))\) qui sont identique et identiquement distribués alors par le théorème central limite nous dit que \(g_{l+1}^i(x)\) suit une loi normale. En appliquant des corollaire du théorème central limite on voit \((\tilde{g}_{l+1}^i(x_1),...,\tilde{g}_{l+1}^i(x_j),...\tilde{g}_{l+1}^i(x_N))\) suit une loi Gaussienne multivariée. Ceci étant vrai pour tout \((x_1,....,x_N)\) on voit que \(\tilde{g}_{l+1}^i(x) =\mathcal{GP}(\mu_l,\Sigma_{l+1})\text{.}\)

\begin{equation*} \mu_l=\mathbb{E}[\tilde{g}_l^i(x)]= \frac{1}{\sqrt{n_l}}\sum_{k=1}^{n_l}\mathbb{E}[\omega_{ik}^l] \sigma(\tilde{g}_k^l)+\beta \mathbb{E}[b_i^l] \end{equation*}

Ensuite on passe à la matrice de covariance:

\begin{align*} \Sigma_l(x,x^{'}) \amp =\mathbb{E}[\tilde{g}_l^i(x)\tilde{g}_l^j(x^{'})] \\ \Sigma_l(x,x^{'}) \amp =\frac{1}{n_l}\mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^l \sigma(\tilde{g}_k^l(x))\right) \left(\sum_{k=1}^{n_1}\omega_{jk}^l \sigma(\tilde{g}_k^l(x))\right)\right]\\ \amp + 2 \frac{\beta}{\sqrt{n_l}}\mathbb{E}\left[\left(\sum_{k=1}^{n_1}\omega_{ik}^l \sigma(\tilde{g}_k^l(x))\right)b_{i}^l +\left(\sum_{k=1}^{n_1}\omega_{jk}^l \sigma(\tilde{g}_k^l(x))\right)b_{j}^l \right]\\ \amp +\beta^2\mathbb{E}\left[b_{i}^l b_j^l\right] \end{align*}

Pour les deux premiers terme on utilise les même arguments que dans le cas \(L=1\text{.}\) Pour le dernier terme on développe

\begin{equation*} \mathbb{E}\left[\left(\sum_{k=1}^{n_l}\omega_{ik}^l \sigma(\tilde{g}_k^l(x))\right) \left(\sum_{k=1}^{n_1}\omega_{jk}^l \sigma(\tilde{g}_k^l(x^{''}))\right)\right]= \langle \sigma(x),\sigma(x^{'}) \rangle \delta_{ij} \end{equation*}

puisque \(\omega^l \sim \mathcal{N}(0,1)\) cela permet de conclure la première partie de la preuve.

Subsubsection 12.4.2.2 Dynamique du NTK

Maintenant on peut introduire les deux résultats principaux de la théorie NTK étudie l'inialisation et la dynamique en temps du NTK durant l'apprentissage. Pour cela on va utiliser le résultat précédent sur le lien avec les processus Gaussien. On va commencer par la caractérisation de l'initialisation.

Théorème 12.5. NTK à l'initialisation.

Soit \(\sigma\) une nonlinarité Lipschitzienne et un réseau \(f_{\theta}\) avec \(L\) couches A la limite \((n_1,....n_{L-1}) \rightarrow +\infty\text{,}\) le NTK \(k_{ij}(x,y)\) converge vers \(k_{\infty}(x,y)\delta_{ij}\) avec \(k_{\infty}\) un noyau déterministe donnée par:

\begin{equation*} k_{\infty}^1(x,y)=\Sigma_{\infty}^1(x,y) \end{equation*}

\begin{equation*} k_{\infty}^l(x,y)=\Sigma_{\infty}^l(x,y)+ k_{\infty}^{l-1}(x,y)\hat{\Sigma}_{\infty}^l(x,y) \end{equation*}

avec

\begin{equation*} \hat{\Sigma}_{\infty}^l(x,y)=\mathbb{E}_{u,v}[\sigma^{'}(u)\sigma^{'}(v)] \end{equation*}

ou \((u,v)\) suit une loi

\begin{equation*} \mathcal{N}\left(0, \begin{pmatrix} \Sigma_{\infty}^{l-1}(x,x) \amp \Sigma_{\infty}^{l-1}(x,y) \\ \Sigma_{\infty}^{l-1}(y,x) \amp \Sigma_{\infty}^{l-1}(y,y) \end{pmatrix}\right) \end{equation*}

Preuve.

Admis

Ce résultat nous assure que a l'initnialisation le noyau NTK, dans la limite ou le nombre de neurone est infini est déterministe et est déterminer par l'architecture du réseau.

Théorème 12.6. NTK durant l'entrainement.

Soit \(\sigma\) une nonlinarité Lipschitzienne et deux fois différentiable et un réseau \(f_{\theta}\) avec \(L\) couches. Pour \(t\in [0,T]\) et \(\forall (x,y)\in\mathbb{R}^{in}\) on a

\begin{equation*} \underset{(n_1,....n_{L-1}) \rightarrow +\infty}{lim} k_{\theta(t)}^L(x,y)=\theta_{\infty}(x,y)I_{out,out} \end{equation*}

Preuve.

Admis

Ce deuxième théorème nous dit, que toujours dans la limite du nombre de neurones infini, le noyau NKT reste constant en temps. On a donc un noyau qui va être déterministe et constant en temps. Cela va nous permettre d'étudier la dynamique de l'apprentissage. Ce résultat est valide uniquement dans la limite \((n_1,....n_{L-1}) \rightarrow +\infty\) mais cette limite approche les régimes sur-paramétré qui est souvent utilisé en pratique. En utilisant ses résultats on peut caractériser la dynamique en temps.

Dynamique en temps du réseau.

Soit un réseau \(f_{\theta(t)}\) à \(L\) couches. Dans la limite \((n_1,....n_{L-1}) \rightarrow +\infty\) on a

\begin{equation*} f_{\theta(0)}\sim \mathcal{N}(0,\Sigma_{\infty}^L) \end{equation*}

\begin{equation*} \frac{d f_{\theta(t)}}{dt}=-\frac{1}{N}\sum_{i=1}^N k_{\infty}(x,x_i) \left( \nabla_{f} l(f,y_i) \right) \end{equation*}

Maintenant on va considérer le cas d'une fonction de coût quadratique. On va travailler en formalisme matricielle. On pose le résultat du réseau \(Y_{\theta(t)}=(f_{\theta(t)}(x_1),...,f_{\theta(t)}(x_1))\text{,}\) les valeurs de référence \(Y\) et la matrice \((K_{\infty}(X,X))_{ij}=k_{\infty}(x_i,x_j)\) alors on a

\begin{equation*} \frac{d Y_{\theta(t)}}{dt}=\frac{2}{N}(Y-Y_{\theta(t)})K_{\infty}(X,X) \end{equation*}

On a donc la solution qui est donnée par:

\begin{equation} Y_{\theta(t)}=Y + ( Y_{\theta(t)}-Y)e^{-t K_{\infty}(X,X)}\tag{12.9} \end{equation}

Puis en moyenne les poids à l'initlisation sont nuls. On a donc

\begin{equation*} \mathbb{E}[Y_{\theta(t)}]=Y (I_d- e^{-t K_{\infty}(X,X)}) \end{equation*}

On voit donc que la dynamique est donc déterminer par le NTK qui est constant en temps. On peut donc etudier le noyau NTK afin de comprendre la dynamique en temps du réseau. Dans [1.27] les auteurs généralisent la méthode NTK aux PINNs sans grande difficulté. Evidemment on obtient une matrice du noyau par fonction de coûts et des matrices qui couplent les fonctions de coûts Maintenant on va montrer a travers des exemples comment l'étude du NTK permet de comprendre certaines qualités ou défauts des réseaux notamment des PINNs.

Subsubsection 12.4.2.3 Biais Spectral

Le biais spectral est une propriété Assemblage des réseaux de type MPC (pouvant être étendu à d'autre type de réseaux) que l'on a introduit précédemment et qui est obtenu par analyse spectral. Ce principe peut être re-obtenu par une approche de type NTK. On se donne la matrice associé au noyau NTK \(K_{\infty}(X,X)\text{.}\) Soit \(v\) un vecteur propre de cette matrice associé a une valeur propre \(d\text{.}\) Le résultat (12.9) couplé a une diagonalisation nous montre que plus \(d\) est grande plus le réseau va apprendre vite dans la direction \(v\text{.}\) Il a été montré sur des exemples que les vecteurs propres associés aux plus grande valeur propres sont des modes a basses fréquences et ceux associés aux petites valeurs propres des modes à hautee fréquences. On retrouve donc bien le problème du biais spectral.

Subsection 12.4.3 Defauts d'entraînement et entraintement modifiés

Dans un certains nombre de cas l'entraînement des PINNs peut ne pas aboutir. Dans [1.22] les auteurs consider des equations d'advection du type:

\begin{equation*} \partial_t u + a\partial_x u = 0 \end{equation*}

de réaction diffusion du type:

\begin{equation*} \partial_t u -D\partial_x u = \rho u(1-u) \end{equation*}

L'enjeu est maintenant de regarder comment l'apprentissage réagit à la variation des paramètres physiques. Pour cela on se fixe un réseau, des paramètres d'entraînement et on regarde comme évolue l'erreur en fonction des paramètres.

Lorsqu'on entraine un PINNs avec des données on peut voir la minimisation comme un problème de moindre carré classique auquel on ajoute une régulisation (fonction coût sur la physique) qui a pour rôle de permettre une généralisation meilleure entre les données. En partant de ce principe les auteurs de [1.22] ont regardé comme la réagissait la fonction coût lorsque cette régularisation devenait de plus en plus grande. Ils ont constatés que plus la régularisation était importante (fonction de coût résiduelle prépondérante) plus la fonction de coût globale devenait peu régulière avec beaucoup de mauvais minimum locaux. De plus, plus les coefficients physiques considérés devenaient importants plus le problème de régularité induit par la fonction de coût physique était important. Globalement pour de grands paramètres si la fonction de coût physique devient trop forte on a une fonction de coût peu régulière et on converge mal. Dans la suite on va parler de plusieurs solutions pour régler ce type de problème.

Subsubsection 12.4.3.1 Méthodes d'homotopie

Les méthodes d'Homotopie de ou de continuation sont des méthodes assez anciennes utilisées pour résoudre des problèmes nonlinéaire difficiles. On se donne un problème du type

\begin{equation*} F(\boldsymbol{u})=0 \end{equation*}

avec \(\boldsymbol{u}\in \mathbb{R}^n\text{.}\) Ce genre de problème est en général résolu par des méthodes itératives de type Newton ou Picard. Si le problème est très fortement nonlinéaire, à moins d'avoir une bonne condition initiale ces méthodes vont converger très lentement ou ne pas converger. Le principe des méthodes d'homotopies est le suivant. On se donne un problème facile à résoudre:

\begin{equation*} G(\boldsymbol{u})=0 \end{equation*}

On peut l'imaginer linéaire ou faiblement nonlinéaire. Ensuite on va construire une application régulière par rapport à l'ensemble de ses variables:

\begin{equation*} H(\boldsymbol{u},t): \mathbb{R}^n\times \mathbb{R}\rightarrow \mathbb{R} \end{equation*}

tel que

\begin{equation*} H(\boldsymbol{u},0)=G(\boldsymbol{u}), \quad H(\boldsymbol{u},1)=F(\boldsymbol{u}) \end{equation*}

On parle d'homotopie car elle déforme continuent la fonction \(G\) en la fonction \(F\text{.}\) Si certaines conditions sont respectées alors si pour \(t \in\mathbb{R}, u(t)\) est solution de \(H(\boldsymbol{u}(t),t)=0\) alors \(x(t)\) est une courbe régulière tel que \(x(0)=G^{-1}(\boldsymbol{0})\) et \(x(1)=F^{-1}(\boldsymbol{0})\text{.}\) La courbe étant régulière on voit bien que plus \(t\) se rapproche de \(1\) plus \(x(t)\) va se rapprocher \(x(1)=F^{-1}(\boldsymbol{0})\text{.}\)

L'idée des méthodes d'homotopie est donc de construire une homotopie en un problème simple et notre problème cible puis d'utiliser la continuité des solutions pour approcher celle du problème cible. Pour cela on utilise l'algorithme suivant:

Algorithm 12.7. Méthode d'homotopie.

On résout \(H(\boldsymbol{u},0)\) ce qui nous donne \(\boldsymbol{u}_0\) et on initialise \(t=0\)
\(\forall 1\le k \lt N_{iter}\text{:}\)
- On résout \(H(\boldsymbol{u}_k,t)\) ce qui nous donne \(\boldsymbol{u}_k\) en utilisant comme condition initiale du solveur \(\boldsymbol{u}_{k-1}\)
- on incrémente la méthode \(t= t+\Delta_t\)
On renvoit \(\boldsymbol{u}_{N_{iter}}\)

Il s'agit d'un algorithme très simple et pouvait être utilisé dans de nombre situation.

Pour revenir au problème d'apprentissage de PINNs pour de grandes valeurs de paramètres d'advection ou de réaction, une façon d'aider l'entraînement est d'utiliser cette approche ("curriculum learning" dans la communauté de l'apprentissage). Par exemple si on prend le problème d'advection l'homotopie est donnée par:

\begin{equation*} H(u(t,x),\beta)=(\partial_t u +a\partial_x u)^{-1}(0) \end{equation*}

Dans le cadre de l'équation d'advection ou la solution est connue on sait que cela revient à

\begin{equation*} H(u(t,x),\beta)=u_0(x-a t) \end{equation*}

On donc ici que la régularité par rapport au paramètre d'homotopie \(a\) dépend uniquement de la régularité de la condition initiale. Pour appliquer Algorithm 12.7, a chaque étape on applique de l'algorithme un apprentissage avec une valeur donnée de \(a\) ou \(\rho\) et on utilise le réseau entrainé à l'étape précédente comme initialisation.

Subsubsection 12.4.3.2 Causalité temporelle et apprentissage adapté

Une autre approche pour améliorer l'apprentissage est de tenir compte de la causalité temporelle. Contrairement aux méthodes numériques classiques, l'approche PINNs calcul l'ensemble des temps en même temps et n'utilise pas le temps précédent pour calculer le temps suivant. On peut appliquer la méthode NTK pour regarder comment l'apprentissage évolue en fonction du temps physique. On définit le noyau continue en temps mais sur les points déchantillon en espace. On obtient \(K_{\infty}(t)\text{:}\)

\begin{equation*} (K_{\infty}(t))_{ij}= \langle \frac{\partial }{\partial \theta}R_{\theta}(t,x_i), \frac{\partial }{\partial \theta} R_{\theta}(t,x_i)\rangle\in \mathcal{M}_{N_x,N_x} \end{equation*}

Puisqu'on sait que ce noyau va être constant le long de l'entrainement dans la limite de sur-paramétrisation, on va pouvoir dire que le taux convergence exponentiel vers la bonne solution sera donnée par

\begin{equation*} C(t)=\frac{tr(K_{\infty}(t))}{N_x} \end{equation*}

Il se trouve que sur un certains nombre d'exemples on remarque que \(C(t)\) est plus grande pour les grands \(t\text{.}\) Ce qui est constaté dans [1.23], Par conséquent le réseau admet un biais implicite qui le pousse à se concentrer sur les derniers temps et à ignorer la causalité temporelle inhérente aux EDP d'évolution.

Pour régler ce problème plusieurs approches sont possibles. La première est d'entraîner le réseau en temps compte de cette causalité. Pour cela on divise utilise aussi une méthode de continuation couplée avec une méthode qui permet de capturer la condition initiale exactement. A l'étape \(k\) de l'algorithme d'homotopie on résout notre problème d'apprentissage avec la fonction de coût suivante:

\begin{equation*} \mathcal{J}_{res}=\int_{k\Delta t}^{(k+1)\Delta t}\mid R_{\theta}(t,x)\mid \end{equation*}

avec \(R_{\theta}(t,x)\) le résidu de l'équation et avec

\begin{equation*} u_{\theta}(t,x)=\hat{u}_{\theta}(k\Delta t,x) +(t-k\Delta t)\hat{u}_{\theta}(t,x) \end{equation*}

avec \(\hat{u}_{\theta}(t,x)\) le réseau et \((t,x)\) les points de collocation de Monte-Carlo tirés aléatoirement dans l'espace \([k\Delta t, (k+1)\Delta t]\times \Omega\text{.}\) Ce choix revient a entraîner le réseau sur un intervalle de en utilisant comme condition initiale (imposé fortement) la solution déterminée sur le précédent interval. On compare l'entraînement classique et ce type d'entraînement sur la figure Figure 12.8.

Figure 12.8. Gauche: entraînement classique, Droite: entraînement causal. Images issues de [1.22].

Pour tenir compte de le causalité temporelle une autre approche est de modifier la fonction de coût résiduelle de façon à ce qu'elle tienne compte de cette causalité. C'est la stratégie proposée dans [1.23]. Pour cela on se donne le résidu local de notre EDP \(r(t,x)\) et on défini la fonction de coût résiduelle de la façon suivante:

\begin{equation*} \mathcal{J}_{res}(\theta)=\frac{1}{N_t}\sum_{i=1}^{N_{t}}\mathcal{J}(t_i,\theta) \end{equation*}

avec

\begin{equation} \mathcal{J}(t_i,\theta)=\sum_{j=1}^{N_{x}}\mid r(t_i,x_j)\mid^2\tag{12.10} \end{equation}

L'idée est d'apprendre un temps que les temps précédents ont été bien appris. Pour cela on utilise une fonction de coût modifiée.

Définition 12.9. Fonction de coût résiduelle causale.

La fonction de coût residuelle suivant est utilisée pour respecter la causalité temporelle:

\begin{equation*} \mathcal{J}_{res}(\theta)=\frac{1}{N_t}\sum_{i=1}^{N_{t}}\omega_i\mathcal{J}(t_i,\theta) \end{equation*}

avec \(\mathcal{J}(t,\theta)\) donnée par (12.10) et

\begin{equation*} \displaystyle\omega_i=e^{-\epsilon\left(\sum_{k=1}^{i-1} \mathcal{J}(t,\theta)\right)} \end{equation*}

Au début de l'apprentissage, puisque le residu est grand partout, la fonction de coût va mettre un poid très petit sur les temps grand. Ensuite plus un temps est correctement appris plus le point des temps suivant se rapproche de \(1\text{.}\) Cela va donc permettre en ajustant les poids de lafonction de coût d'apprendre progressivement en partant des premiers temps jusqu'aux derniers.

Subsubsection 12.4.3.3 Autres type de biais

La méthode NTK a permis d'exhiber d'autres types de biais qu'on va rapidement décrire ici. Par exemple pour des EDP elliptique [1.26] fortement oscillantes (ref):

\begin{equation*} -\frac{d}{dx}\left(a(\frac{x}{\epsilon})\frac{d}{dx} u(x) \right)=f(x) \end{equation*}

L'analyse du NTK montre que la matrice \(K_{\infty}(X,X)\) admet un facteur multiplicatif \(\frac{1}{\epsilon^2 N_x}\) ce qui montre que si le nombre de points n'est pas pris comme \(N_x\approx \frac{1}{\epsilon^2}\) alors la convergence des poids va être lente. Maintenant si on regarde une équation d'advection diffusion du type:

\begin{equation*} \partial_t u +\beta \partial_x=D \partial_{xx} u \end{equation*}

Les auteurs d'un papier [1.25] on étudié le NTK dans les régimes advectifs et diffusifs pour un PINNs sans données. Dans les régime advectif et diffusif il remarque que plus \(\beta\) ou \(D\) sont grands plus l'influence dans le noyau NTK de la fonctions coût est grande par rapport aux fonctions de coûts sur les conditions initiales et aux bors. Par conséquent le convergence vers zéro du résidu semble bien plus rapide, par conséquent il n'apprend pas les conditions limites et aux bords. Dans ce cas le problème devient un peu mal posé et il apprend donc une solution très éloignée de la bonne. Ils remarquent aussi que comme attendu le biais spectral apparait notamment pour les problèmes ou l'advection est dominante.

Subsection 12.4.4 PINNs pour des EDP Paramétriques

Lorqu'on entraine un réseau physiquement informé on résout une EDP. Un entrainement est donc équivalent à l'utiliser d'un solveur de type élement ou différence finis. En pratique on peut rapidement constater que cette approche est peu compétitive par rapport à une méthode numérique standard (ref) notamment en 1D et 2D. Cependant le PINNs possèdent deux avantages importants sur les approches classiques. Il ne néncessite pas de maillage et est peu sensible à la dimension puisqu'il combine réseaux de neurones et intégration de Monte-Carlo. Il devient donc de plus en plus competitif lorsque la dimension augmente. Afin de tirer partie d'approche comme les PINNs il est donc souhaitable d'attaquer des problèmes en grande dimension. L'approche basée sur les PINN's introduite dans (ref sun2020surrogate) consiste finalement a calculer non pas une solution classique mais une solution paramétrique de type \(\mathbf{U}_{\theta}(t,x,\boldsymbol{\mu})\) à l'aide d'un PINNS. Une fois cette solution approchée d'une EDP paramétrique, on peut très rapidement obtenir une solution pour un jeux de paramètres \(\boldsymbol{\mu}\) donné. D'abord on définit la solution:

\begin{equation*} \hat{\mathbf{U}}_{\theta}(t,x,\boldsymbol{\mu})=\mathbf{U}_{par}(t,x,\boldsymbol{\alpha}) +\psi(t,x)\mathbf{U}_{\theta}(t,x,\boldsymbol{\mu}) \end{equation*}

avec

\begin{equation*} \mathbf{U}_{par}(t,x)= \chi_{\left\{t=0\right\}}\mathbf{U}_0(x,\boldsymbol{\alpha})+\chi_{\left\{x\in \partial \Omega \right\}}g(x) \end{equation*}

Ensuite on introduit la loss a minimiser:

\begin{equation*} \mathcal{J}(\theta)=\int_{V_{\mu}}\int_0^T\int_{\Omega}\parallel \partial_t\mathbf{U}_{\theta}(t,x)- \mathcal{L}(\mathbf{U}_{\theta},\partial_x \mathbf{U}_{\theta}, \partial_{xx} \mathbf{U}_{\theta},\boldsymbol{\beta})(t,x) \parallel_2^2 dxdt d\boldsymbol{\mu} \end{equation*}

Pour conclure l'approche il suffit donc d'échantillonner l'espace des paramètres comme l'espace physique. En pratique on utilise une méthode Monte-Carlo.