Opérateur neural et approche spectrale

Section 13.5 Opérateur neural et approche spectrale

Comme on l'a déjà introduit principalement la principal difficulté dans la construction d'une couche de neural opérateur Définition 13.7 - Définition 13.10 est de construire une version discrète la plus général possible de l'opérateur de convolution a noyau. Ici on va détailler les approches qui utilise des version spectrales ou partiellement spectrales de la convolution.

Subsection 13.5.1 FNO Classique

On va donc se concentrer sur l'opérateur

\begin{equation} u(x)=\int_{\Omega}k(x,y)v(y) d\nu(y) \tag{13.4} \end{equation}

on va supposer que l'on prend un noyau invariant par rotation de la forme:

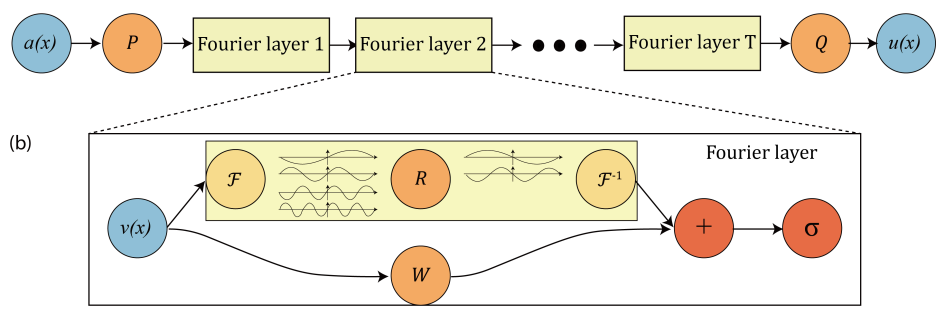
\begin{equation*} k(x,y)=k(x-y) \end{equation*}

Si on utilise ce type de noyau on reconnait que (13.4) est une convolution entre les fonction \(k\) et \(v\text{.}\) La convolution est peut être aussi définit dans l'espace de Fourier.

Définition 13.12. Convolution dans l'espace de Fourier.

Soit une convolution

\begin{equation*} (f \star g)=\int_{\Omega}f(x-y)g(y) dy \end{equation*}

peut être définie à partir de la transformée de Fourier \(\mathcal{F}\) par

\begin{equation*} (f \star g)= \mathcal{F}^{-1} (\mathcal{F}(f)(k) \mathcal{F}(g)(k)) \end{equation*}

avec \(k\) la variable dans l'espace de Fourier/

L'idée centrale des FNO est tout simplement d'utiliser la définition spectrale de la convolution pour approcher ce produit. En pratique on va apprendre directement la transformé de Fourier de notre noyau. Cela nous permet de définir une couche d'un réseau FNO.

Définition 13.13. Formulation continue d'une couche FNO.

On appelle une couche FNO au sens continue: une fonction qui transforme une fonction \(v_t(x)\in \mathbb{R}^{d_t}\) en une fonction \(v_{t+1}(x)\) au point \(x\in D\) de la forme:

\begin{equation*} v_{t+1}(x) = \sigma_{t+1}\left( W_t v(x)+ b(x) + \mathcal{F}^{-1} ( R_{\theta}(k) \mathcal{F}(v)(k) ) \right) \end{equation*}

avec \(R_{\theta}(k)\in \mathcal{M}_{d_t,d_{t+1}}\) la transformée de fourier d'un opérareur \(k: D\rightarrow \mathbb{C}^{(d_{t+1})\times d_t}\text{,}\) \(W_t \in \mathcal{M}_{d_{t+1},d_t}(\mathbb{R})\) et \(b(x) \in \mathbb{R}^{d_{t+1}}\text{.}\)

En pratique cette couche ne peut pas être implémenter. En effet on va travailler sur des fonctions discretisée. On va donc avoir accès aux fonctions \(v_t(x), b(x)\) sur un nombre de points déterminés \((x_1,...,x_n)\text{.}\) La partie linéaire des couches a été introduite précédemment. On va détaille la partie nonlocal.

On se donne une fonction \(v_t(x)\in \mathbb{R}^{d_t}\text{.}\) Si on discrétise cette fonction avec \(n\) points on obtient \(V_{t}\in \mathcal{M}_{n,d_t}(\mathbb{C})\text{.}\) Si on donne au maximum \(k_{max}\) modes de fourier et qu'on applique une FFT \(\mathcal{F}_{ftt}\) on obtient:

\begin{equation*} \mathcal{F}_{ftt}(v_{h,t}) \in \mathcal{M}_{k_{max},d_t}(\mathbb{C}) \end{equation*}

Ensuite on applique notre filtre qu'on apprend directement en Fourier: \(R_{d,\theta}\in \mathbb{C}^{k_{max},d_{t+1},d_t} \) Avant d'appliquer notre FFT inverse. En pratique on choisit \(k_{max}= (k_{loc}^m)^d\) avec \(k_{loc}^m\) le nombre maximal de modes par direction spatiale.

Définition 13.14. Couche FNO.

On appelle une couche FNO: une fonction qui transforme une fonction discrete \(V_t=(v_t(x_1),...,v_t(x_n) )\in \mathcal{M}_{n,d_t}(\mathcal{C})\) en une fonction discrete \(V_{t+1}=(v_{t+1}(x_1),...,v_{t+1}(x_n))\in \mathcal{M}_{n,d_{t+1}}(\mathbb{C})\text{:}\)

\begin{equation*} v_{t+1}(x_i) = \sigma_{t+1}\left( W_t v_t(x_i)+ b + \mathcal{F}_{fft}^{-1} ( R_{\theta}(k) \mathcal{F}_{fft}(V_t) )(x_i) \right) \end{equation*}

avec les paramètres à apprendre: \(R_{d,\theta}\in \mathbb{C}^{k_{max},d_{t+1},d_t}\text{,}\) \(W_t \in \mathcal{M}_{d_{t+1},d_t}(\mathbb{R})\) et \(b \in \mathbb{R}^{d_{t+1}}\text{.}\)

La complexité de cette couche est principalement liée à celle de la FFT on a donc une complexité en \(O(n log n )\text{.}\) Comme on a montrer que les parties linéaires ne vont pas déprendre de la discrétisation c'est la même chose pour la partie non locale. En effet les filtres appris ne vont pas dépendre de la discrétisation puisqu'on apprend dans l'espace de Fourier. Cependant on est limité à des grilles régulières pour utiliser la FFT.

Figure 13.15. Fonctionnement d'un réseau FNO.

Le fonctionnement d'un FNO est détaillé sur l'image Figure 13.15.

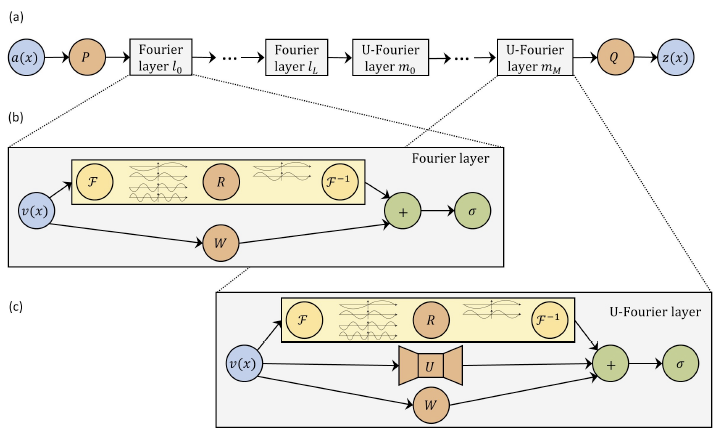
Il existe une variante des réseaux FNO appelée U-FNO ou on ajoute un terme dans la couche qui est un Unet et va se concentrer sur les hautes fréquences.

Définition 13.16. Couche UFNO.

\begin{equation*} v_{t+1}(x_i) = \sigma_{t+1}\left( W_t v_t(x_i)+ b + \mathcal{F}_{ftt}^{-1} ( R_{\theta}(k) \mathcal{F}_{ftt}(V_t) )(x_i) + UNet_{\theta}(V_t)(x_i) \right) \end{equation*}

avec les paramètres a apprendre: \(>R_{d,\theta}\in \mathbb{C}^{k_{max},d_{t+1},d_t}\text{,}\) \(W_t \in \mathcal{M}_{d_{t+1},d_t}(\mathbb{R})\text{,}\) \(b \in \mathbb{R}^{d_{t+1}}\) et\(\theta\) les paramètres d'un réseaux convolutif unet\(UNet_{\theta}\text{.}\)

Figure 13.17. Fonctionnement d'un réseau U-FNO.

Le fonctionnement d'un U-FNO est détaillé sur l'image Figure 13.17. Cependant l'introduction de cette partie Unet ne permet plus d'obtenir un réseau capable de traiter une grille de taille arbitraire.

Pour gérer le temps il existe plusieurs solution. Une première est d"utiliser un opérateur neural de type FNO pour prédire le temps final. Une seconde solution est de considérer le temps comme une feature. Par exemple on va donné en entrée \(m\) données temporelles entre \([0,T]\) et on demande au réseau de prevoir un certains nombre de solutions a des temps selectionné entre \([T,T_2]\text{.}\) La dernière solution est de considérer la dimension temporelle de la même façon que la dimension spatial.

Subsection 13.5.2 FNO Sur des géométries générales

En construction

Subsubsection 13.5.2.1 FNO

En construction

Subsubsection 13.5.2.2 FNO de vandermonde

En construction

Subsection 13.5.3 FNO Sur des variétés Riemannienne

Comme il est introduit dans le chapitre 1, on généraliser l'analyse de Fourier a des variétés. En effet il suffit de calculer les vecteurs propres de l'opérateur de Laplace Beltrami et de les utiliser comme base de Fourier. En effet de la même façon il vont permettent d'obtenir une base de plus en plus oscillante ou les modes sont associés à des fréquences de plus en plus grande. Comment introduit dans le chapitre 1 on peut calculer une approximation de cet opérateur de Laplace-Beltrami sur une maillage ou sur un graphe de voisinage associés a des points de la variété. Le théorème .... nous indique que l'on converge en fonction du nombre de points vers le vrai opérateur de Laplace Beltrami. Autrement dit si la résolution est suffisante les vecteurs propres du laplacien vont être assez invariant au changement de résolution et du maillage locale (on a aussi vu cela dans le chapitre sur les GNN). Par conséquent, on peut apprendre des filtres dans l'espace de Fourier associé aux vecteurs propres du Laplacien sur graphe \(P_h\) et ses filtres resteront valable par changement de maillage et de résolution (si elle est suffisemment grande). C'est ce qui est proposé dans le papier [1.31].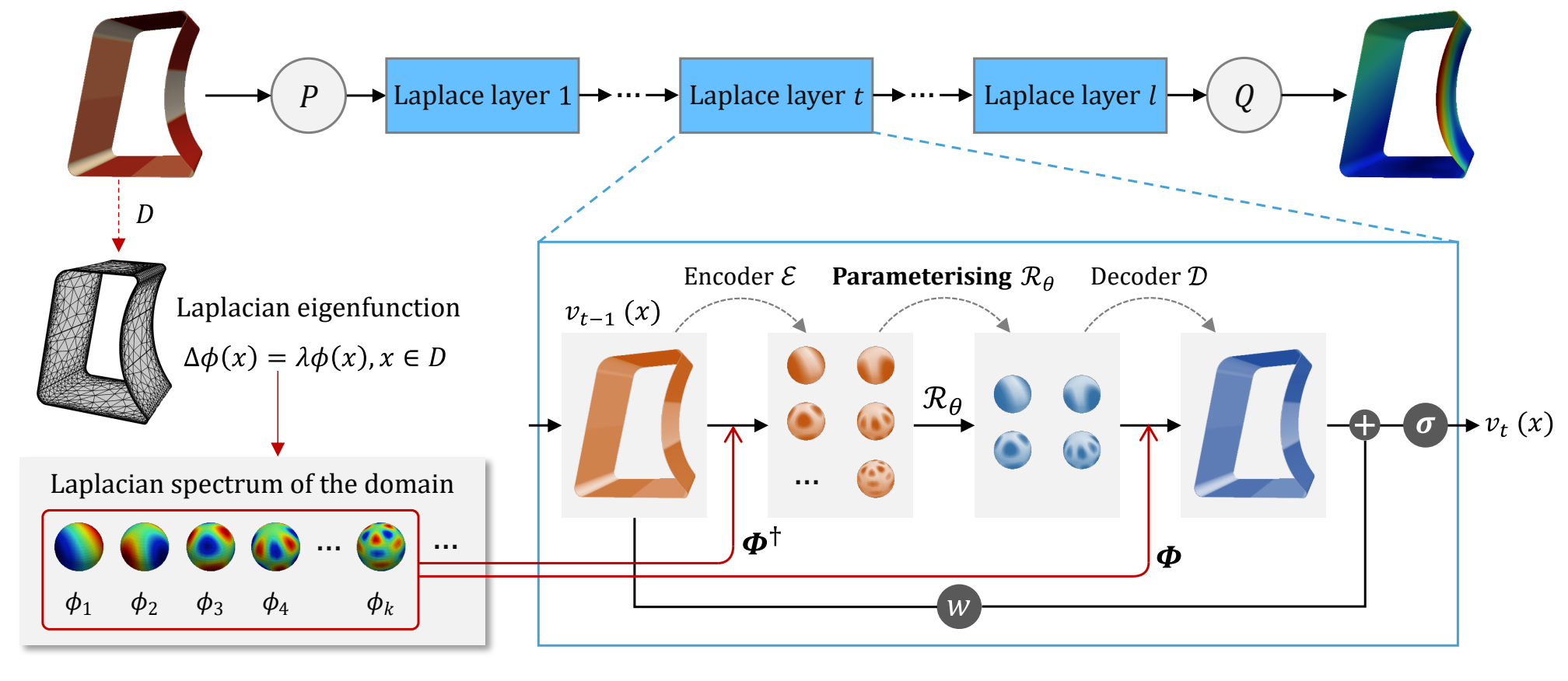

Figure 13.18. Fonctionnement d'un réseau FNO.

Le principe est représentée sur la figure Figure 13.18 du papier [1.31]. Il s'agit donc de a généralisation naturelle du FNO a des variétés Riemannienne grace à la théorie de graphe Laplacien. Cette approche est presque la même que celle introduite dans le premier GNN spectral. Pour les GNN ne n'était pas satisfaisant car le cout de changement de bases était très important et que les applications étant différente on cherchait des filtres très localisés en espace (comme en traitement du signal) et aller recuperer la non localité en déraffinant progréssivement. En effet cette approche, qu'on S. Mallat relie a la notion de séparation d'échelle semble importante pour les problèmes d'imageries. Ici a l'inverse on sait qu'on doit aller capturer des problèmes très non locaux et donc conserver cette approche est intéressante. Cependant le calcul du changement de base reste un point limitant et le réseau comme le FNO est utilisé avec un nombre faible de couches.

Subsection 13.5.4 Opérateur Neural et ondelette

En construction

Subsection 13.5.5 Opérateur Neural et transformé de Laplace

En construction

Subsection 13.5.6 Unification des approches spectrales

En construction