Section 17.2 Méthodes d'hyper réduction
TOO DOO
Si on se replace dans le cadre simple de la projection de Galerkin (ce serait similaire pour une autre projection), on se retrouve avec un terme nonlinéaire a estimer dans l'espace réduit. Par exemple dans le cas de la projection de type Galerkin on a:
Estimer ce terme nécessite de remonter dans l'espace complet en appliquant \(\Phi_K\) et de redescendre dans l'espace réduit avec \(\Phi_K^{T}\text{.}\) En termes de complexité on a
\(\displaystyle \Phi_K \hat{\bs{x}} \approx O(n K)\)
\(\displaystyle \Phi_K^t \bs{f} \approx O(n K)\)
\(\displaystyle \bs{f}(\tilde{\bs{x}}) \approx O(n^2)\)
Puisque qu'on suppose \(K \lt \lt n\) c'est le dernier terme qui pause vraiment problème. Si on fait cela a chaque pas de temps, le cout de calcul risque d'être similaire à la résolution du problème en grande dimension.
Il faut donc construire le flux nonlinéaire pour l'espace réduit. À ce moment-là il existe deux cas de figure:
on sait l'écrire analytiquement,
on ne sait pas le construire analytiquement et on doit construire une approximation, on parle d'hyper-reduction.
Dans le cas de Burgers on va pouvoir écrire la nonlinearité analyiquement. On va d'abord écrire dans un cadre un peu plus général dans d'introduire pour la culture générale des méthodes d'hyper réduction.
On va juste définir avant l'opérateur \(\otimes\) qui sera ici le produit de Kronecker rangé par colonne. Donc si \(\bs{b}\in \mathbb{R}^n\text{:}\)
Si B une matrice telle que \(B=[\bs{b}_1,...\bs{b}_K]\in \mathcal{M}_{n,K}(\mathbb{R})\) alors
Lemme 17.19.
Soit un modèle du type
avec \(A\in \mathcal{M}_{n,n}\) et \(B\in \mathcal{M}_{n,n^2}\text{.}\) Alors la projection de Galerkin dans le cas \(\bs{x}_{ref}=0\) est donné par le modèle suivant:
avec \(\hat{A}=\Phi_K^{T} A \Phi_K\text{,}\) \(\hat{B}=\Phi_K^{T} B (\Phi_K \otimes \Phi_K)\) ou \(\hat{C}=\Phi_K^{T} C (\Phi_K \otimes \Phi_K \otimes \Phi_K)\)
On admet il s'agit juste de calcul matriciel assez lourd. Les discrétisations classiques de Burgers (schémas VF classiques, schémas élément finis) rentrent dans ce cadre. Évidemment dans le cadre de méthode de VF, la matrice \(B\) est très creuse.
Dans le suite on va se placer dans le cas d'une nonlinearité générale et voir comment la traiter.
Subsection 17.2.1 Méthode Gappy POD
La méthode Gappy-POD est la première approche pour estimer une nonlinearité en dimension réduite en évitant un calcul coûteux. On connaît de snapshots, par exemple (17.11) dans le cas de la POD (marche aussi pour des snapshots de type DMD). On donc calculer des snapshots qui estime la non-linéarité \(\bs{f}\) en les snapshots d'origine. Puisqu'on a possède ses snapshots
On peut appliquer une POD à ces nouveaux snapshots qui est solution du problème de régression
On reviendra plus en détail plus tard sur l'existence et l'unicité des solutions de ce type de problème. Ici on va admettre les résultats. Maintenant on va donner une matrice d'échantillonnage \(Z=\left[e_{i_1},...e_{i_l}\right]\in \mathcal{M}_{n,l}(\mathbb{R})\) Cette matrice à pour rôle de sélectionner \(l\) indices du vecteur qu'elle multiplie.
L'idée de la méthode Gappy-POD est de trouver la représentation dans l'espace réduit d'un vecteur \(\bs{f}_x\) qui minimise l'erreur de reconstruction seulement sur certains indices. Cela revient donc a résoudre
Il s'agit d'un problème de type moindre carré donc la solution est donnée par l'équation normale (chapitre 2). On a donc
La nonlinearité réduite ici est donc estimée
En grande dimension on obtient l'approximation
On obtient donc la formule d'hyper réduction qui estime la nonlinearité de la méthode de Galerkin
Hyperduction Gappy-POD.
Le vecteur nonlinéaire de dimension \(K\) du modèle (17.23) est estimé par
avec \(A^{+}=(A^t A)^{-1}A\) le pseudo-inverse de Penrose.
La matrice \(G\) peut évidement être précalculée en amont. En termes de complexité on a
\(\displaystyle \Phi_K \hat{\bs{x}} \approx O(n K)\)
\(\displaystyle B \bs{}_z \approx O(K l)\)
\(\displaystyle Z^t\bs{f}(\tilde{\bs{x}}) \approx O(l)\)
On voit que si \(l\ge K\) est du même ordre que \(K\) On obtient une complexité de calcul linéaire en \(O(n)\) au lieu de quadratique. Cependant on aimerait se débarrasser totalement de la dépendance en \(n\text{.}\) En général dans ce cas, on sépare les parties linéaire et nonlinéaire. On a par exemple (17.2) qui devient:
Dans ce cas la réduction de type Galerkin devient
avec \(\hat{A}=\Phi_k^t A \Phi_k\text{.}\)
On peut, à ce moment-là, différencier plusieurs cas:
le cas ou \(\bs{g}(\bs{x})=(g(x_1),....,g(x_n))^t\text{.}\) C'est typiquement le genre de non-linéarité qu'on obtient lorsqu'on discrétise une source nonlinéaire. Ici on peut remarquer que si on applique une méthode POD Gappy à \(\bs{g}\text{.}\) Alors
\begin{equation*} Z^t \bs{g}\left(\bs{x}_{ref}+\Phi_K \hat{\bs{x}}\right)= \bs{g}\left(Z^t (\bs{x}_{ref}+\Phi_K \hat{\bs{x}})\right) \end{equation*}On a donc, dans ce cas, une complexité en \(O(lK)\) pour estimer la non-linéarité.le cas ou \(\bs{g}(\bs{x})=B \bs{g}_l\) avec \(\bs{g}_{l}(\bs{x})=(g(x_1),....,g(x_n))^t\text{.}\) Ce cas se retrouve avec une discrétisation centrée ou élément finis d'un terme du type \(\partial_x^{p} g(\rho)\text{.}\) Dans ce cas on réécrit la réduction sous la forme:
\begin{equation*} \Phi_k^t B \bs{g}_{loc}(\bs{x}_{ref}+\Phi_k\bs{x}(t),\bs{\mu})= \hat{B} \Phi_k^t \bs{g}_{loc}(\bs{x}_{ref}+\Phi_k\bs{x}(t),\bs{\mu}) \end{equation*}avec \(\hat{B}=\Phi_k^t B\Phi_k\) et on applique la stratégie du cas précédent à \(\bs{g}_{loc}\text{.}\) On a dans ce cas une estimation de la nonlinarité en \(O(lK^3)\text{.}\)Le cas ou \(\bs{g}(\bs{x})=(g_1(x_{1},...,x_{\alpha}),...,g_i(x_{i-\alpha},...,x_{i+\alpha}),...))^t\text{.}\) C'est à dire ou le vecteur est assez parcimonieux. C'est ce qu'on peut avoir de plus général pour une EDP nonlinéaire locale (pas de terme intégral). Calculer le terme \(Z^t \bs{g}\left(\bs{x}_{ref}+\Phi_K \hat{\bs{x}}\right)\) revient juste à calculer certaine ligne de \(\bs{g}\left(\bs{x}_{ref}+\Phi_K \hat{\bs{x}}\right)\text{.}\) Pour calculer ces lignes on peut donc calculer le produit \(\Phi_K \hat{\bs{x}}\) que pour les \(2\alpha\) dont on a besoin. On a donc un produit en \(O(2\alpha K)\) et une estimation de la non-linéarité en \(O(2\alpha K l)\text{.}\) On peut retrouver des détails dans [1.4].
Exemple 17.20.
On reprend l'exemple (17.1). Quelle est la forme de l'EDO et comment la traiter ?
Si on discretise le terme de diffusion avec un schéma classique et le terme de Burgers avec un schéma de type local Lax-Friedrichs et des conditions limites périodiques. On note \(\bs{x}\) la densité \(\rho\) discrètisée sur le maillage. On obtient:
avec \(D_{2h}\) la matrice de la dérivée discrète centrée, \(D_{h}\) la matrice de la dérivée discrète décentrée amont, \(\bs{f}(\bs{x})=(x_1^2,.....,x_n^2)\) et \(\bs{g}(\bs{x})=(max(x_n,x_1),..,max(x_i,x_{i+1}),...,max(x_n,x_1))\text{.}\)
On pose
On obtient
avec \(\bs{g}_2(\bs{x})= (\bs{g}(\bs{x})D_h (\bs{x}))\text{.}\) Cette linéarité est parcimonieuse donc peut être rapidement évaluée. On reconstruira \(\bs{x}_{ref}+\Phi_K \hat{\bs{x}}\) que autour des indices sélectionnés par \(Z^t\text{.}\)
Subsection 17.2.2 Méthode DEIM
La méthode DEIM (Discrete Empirical Interpolation Method) est probablement la plus courante pour construire une hyper réduction. Le principe est similaire à la méthode Gappy-POD mais propose de remplacer la régression (17.42) sur des points sélectionnés par \(Z\) par une interpolation.
On se donne une non-linéarité \(\tilde{\bs{g}}(\bs{x})\) Cela veut dire que pour certains points (représentée par \(Z\) que une nonlinearité approchée \(\tilde{\bs{g}}(\bs{x})\) :
On applique une POD au snapshots de la non-linéarité qui donne \(\Phi_k^f\text{.}\) On a donc
avec \(l=K\) le nombre de points d'interpolation. Si on suppose que la matrice est inversible. On obtient
et donc
On va maintenant appliquer cela à notre non-linéarité \(\Phi_K^t \bs{f}\left(\bs{x}_{ref}+\Phi_K \hat{\bs{x}}\right)\)
Hyperduction DEIM.
Le vecteur nonlinéaire de dimension \(K\) du modèle (17.23) est estimé par
avec \(Z\in \mathcal{M}_{K,l}(\mathbb{R})\)
la matrice qu'on appelle le le projecteur oblique.
Maintenant se pose la question de la sélection des indices d'interpolation donc de la construction de \(Z\) et peut-on avoir des garanties sur la méthode.
Pour construire les points l'idée est la suivante. On va faire une approche gloutonne. On va cherche le meilleur indice au sens ou celui qui maximise l'erreur d'interpolation sur un mode de la SVD. Donc l’ indice serait choisi pour minimiser l'erreur de reconstruction du premier mode (celui à la valeur propre la plus grande) puis le second indice pour reconstruire au mieux le second mode, etc. On va supposer par la suite que les vecteurs de \(\Phi_k\) sont ordonnés par valeur propre décroissante. On obtient l'algorithme suivant.
Algorithm 17.21. Algorithme Glouton hors-ligne pour DEIM.
On initialise la base : \(\Phi^f=[\bs{\phi}_1]\)
On initialise la matrice des indices: \(Z=[\bs{e}_{i_1}]\) avec
\begin{equation*} i_1=\underset{i\in\left\{1,...,n\right\}}{\operatorname{argmax}}\mid (\bs{\phi}_1)_i\mid \end{equation*}-
pour \(l=2\) et \(l\leq K\text{:}\)
On calcul l'interpolation du vecteur \(\bs{\phi}_{l}\) en résolvant
\begin{equation*} Z^t \Phi^f \bs{s} = Z^t \bs{\phi}_{l} \end{equation*}On calcul le résisu sur l'interpolation de \(\phi_{l}\)
\begin{equation*} \bs{r} =\bs{\phi}_{l} -\Phi^f \bs{s} \end{equation*}On calcul le nouvelle indice avec
\begin{equation*} i_l=\underset{i\in\left\{1,...,n\right\}}{\operatorname{argmax}}\mid \bs{r}_i\mid \end{equation*}On initialise la matrice des indices: \(Z=[e_{i_1},...e_{i_l}]\)
On incrémente la base \(\Phi^f=[\bs{\phi}_1,..,\bs{\phi}_{l}]\)
On renvoie \(Z\)
On va maintenant introduire quelques résultats rapides sur la méthode DEIM. On commence par définir précisément l'approximation de type DEIM dans un contexte général.
Définition 17.22.
Soit une fonction \(\bs{f}:V\in \mathbb{R}^d\rightarrow \mathbb{R}^n\text{.}\) On se donne des vecteurs de \(\mathbb{R}^n\) \(\Phi=(\bs{\phi},...,\bs{\phi}_K) \) linéairement indépendant. Pour un point \(x\in V\) l'approximation DEIM est donnée par
et \(Z=(\bs{e}_{i_1},...,\bs{e}_{i_K}) \text{.}\)
La méthode est déterminée uniquement par la base de projection \(\Phi=(\bs{\phi},...,\bs{\phi}_K)\) car en effet les points d'interpolation sont choisis de façon à minimiser l'erreur de reconstruction de la base en elle-même. La précision de la méthode dépend donc particulièrement de \(\Phi\text{.}\) On va maintenant introduire une estimation d'erreur sur la méthode. Sur la figure Figure 17.23 on voit la progression de l'algorithme en terme se sélection de point lorsqu'on utilise une base composée des 6 premiers modes de Fourier.
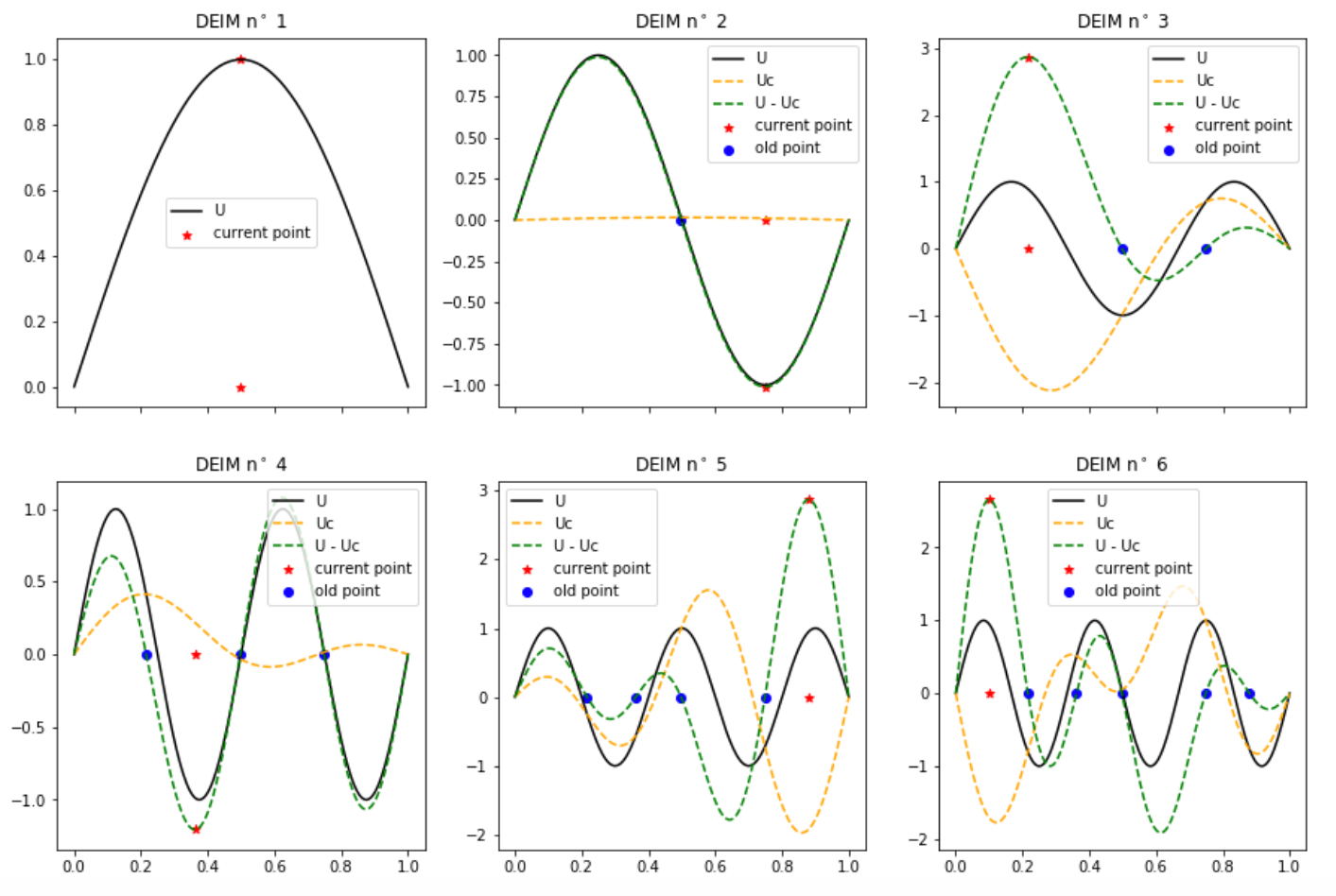
Lemme 17.24.
On se donne une approximation donnée par Définition 17.22 avec \(\bs{f}\) un vecteur de \(\mathbb{R}^n\) cette fois (une discrétisation de notre fonction d'origine) et avec \(\Phi\) une matrice orthogonale alors
On peut donner la majoration suivante
Preuve.
La meilleure approximation de \(\bs{f}\) sur l'espace \(\operatorname{Vect}(\Phi)\) est donné par \(\bs{f}_{opt}= \Phi\Phi^t\bs{f}\text{.}\) On reconnaît la matrice de la projection orthogonale sur \(\operatorname{Vect}(\Phi)\text{.}\) On écrit
On considère notre approximation maintenant
On remarque que
donc
En utilisant (17.45) - (17.46) on obtient que
On passe à la norme et on obtient que
Dans [1.5] on obtient l'identité:
Et ensuite on peut majorer cela
Puisque \(\Phi\) et \(Z\) (permutation des \(K\) vecteurs de la base canonique de \(\mathbb{R}^n\)) on obtient bien (17.43).
Maintenant l'enjeu est de majorer le terme \(\Norm (Z^t \Phi)^{-1}\Norm_2\text{.}\) Ce terme dépend des indices sélectionnés par \(Z\) qui dépendent eux-mêmes de la base par l'algorithme de construction. On va introduire des notations:
et
On considère maintenant \(M=Z^t \Phi\) et on va étudier la norme de l'inverse au fur et à mesure de l'algorithme de construction. A la première itération on a
Il est facile de voir que \(\Norm M^{-1}\Norm_2= \frac{1}{\mid \bs{e}_{i_1}^t \bs{\phi}_1\mid } = \Norm \bs{\Phi}_1\Norm_{\infty}^{-1}\text{.}\) Cela est dû au fait que l'indice \(i_1\) est justement choisi comme celui de la plus grande composante de \(\bs{\Phi}_1\text{.}\) On va maintenant procéder par récurrence et considère l'étape \(l\) de l'algorithme. On écrit la matrice de l'étape \(l\text{:}\)
avec \(\bar{M}= \bar{Z}^t\bar{\Phi}\) On va appliquer une décomposition (de type complément de Schur):
avec
On reconnaît le résidu qu'on utilise pour déterminer les indices de l'algorithme Algorithm 17.21.
On peut réécrire cette décomposition sous la forme
Puisque la matrice est orthogonale (donc elle et sont inverse sont de normes un) on a que
Ce qui nous donne la majoration de (17.47):
A partir de la on voit que
car \(\bar{\Phi}\) est orthogonale et \(\bs{e}_{i_{l}}\) un vecteur de la base canonique. On remarque aussi \(\Norm \bar{\Phi} (\bar{M}^{-1}\bar{Z}^t\bs{\phi}_l)-\bs{\phi}_l\Norm_2=\Norm\bs{r}\Norm_{\infty}\) et que \(\mid (\bs{e}_{i_{l}}^t\bs{r})\mid=\Norm\bs{r}\Norm_{\infty}\) on a donc
En appliquant cette inégalité de façon itérative on obtient le résultat.
L'estimation d'erreur nous apprend déjà que l'erreur est téléguidée par l'erreur de reconstruction associée à la base \(\Phi\text{.}\) Si cette base a été construite par POD on sait que son erreur est reliée à la somme des valeurs propres dont les vecteurs propres n’ont pas été sélectionnés dans la base.
Subsection 17.2.3 LSPG et méthode GNAT
jusqu’à présent on a regarder des méthodes d'hyper réduction qui s'appliquait plutôt la méthode de Galerkin LSG. Cependant on a besoin de méthode d'hyper réduction pour la méthode LSPG. L'approche GNAT applique les idées de la GAPPY-POD mais au lieu de calculer avec non-linéarité réduite issue de la méthode de Galerkin on utilise pour calculer un résidu réduit directement. Cela peut s'appliquer à la méthode LSG (résidu continu en temps).
On crée donc une base de de snapshots du résidu \(\bs{r}^n\) et ensuite on applique une POD qui nous donne la base \(\Phi_r\text{.}\) En appliquant la méthode GAPPY-POD au résidu on obtient:
Donc dans la méthode GNAT, on minimise le problème suivant
A partir de la il y a deux cas: soit on utilise le résidu continu (méthode LSG) ou un résidu discret (méthode LSPG). La solution de (17.48) pour le résidu continu (17.20) est donné par avec
Proposition 17.25. Méthode GNAT pour LSG.
Preuve.
On chercher a minimiser le problème:
On pose \(A=\left(\left( Z^t \Phi_r\right)^{+} Z^t \Phi_K\right)\) et on développe:
On calcul le gradient
On résout maintenant \(\frac{\partial h(\hat{\bs{v}})}{\partial \hat{\bs{v}}}=0\text{.}\) On voit qu'on a la pseudo-inverse de \(A\) qui apparait et on conclut.
Si on considère le un résidu discret (méthode LSPG). On procède différemment. L'approche consiste ensuite à résoudre (17.48) avec le résidu discret (17.32) cela avec une méthode de Gauss-newton (on linéarise à l'intérieur de la norme pour se ramener un problème de moindre carré). Lorsqu'on applique cette méthode on obtient \(\bs{w}^{k+1}=\bs{w}^{k}+\Delta \bs{w}^{k}\)
avec la Jacobienne:
et
On peut calculer la solution de ce problème par l'équation normale puisqu'on a problème de type moindre carrés. On le résout souvent aussi en utilisant une méthode QR sur \(J(\bs{w})\text{.}\)
Subsection 17.2.4 Méthode MPE
En construction: La méthode MPE (Missing Point Esimation) est une autre des approches classiques pour l'hyper réduction.
Subsection 17.2.5 Méthodes d'hyper réduction et apprentissage profond
Conclusion.
Dans cette section, on a défini comment construire un décodeur et un encodeur (réduction), comment construire le modèle réduit (méthodes LSG et LSPG) et comment calculer une nonlinearité ou un second membre dans l'espace réduit pour limiter le temps de calcul. Avec l'ensemble de ces outils, on obtient un ensemble complet pour obtenir un modèle réduit. Par la suite on va voir la limite de ses approches pour des EDP hyperboliques.