Théorie des ondelettes

Section 2.2 Théorie des ondelettes

...

Subsection 2.2.1 Introduction aux ondelettes 1D

L'analyse de Fourier est un outils fondamental en EDP comme en traitement de signal. Cependant elle admet certaines limites.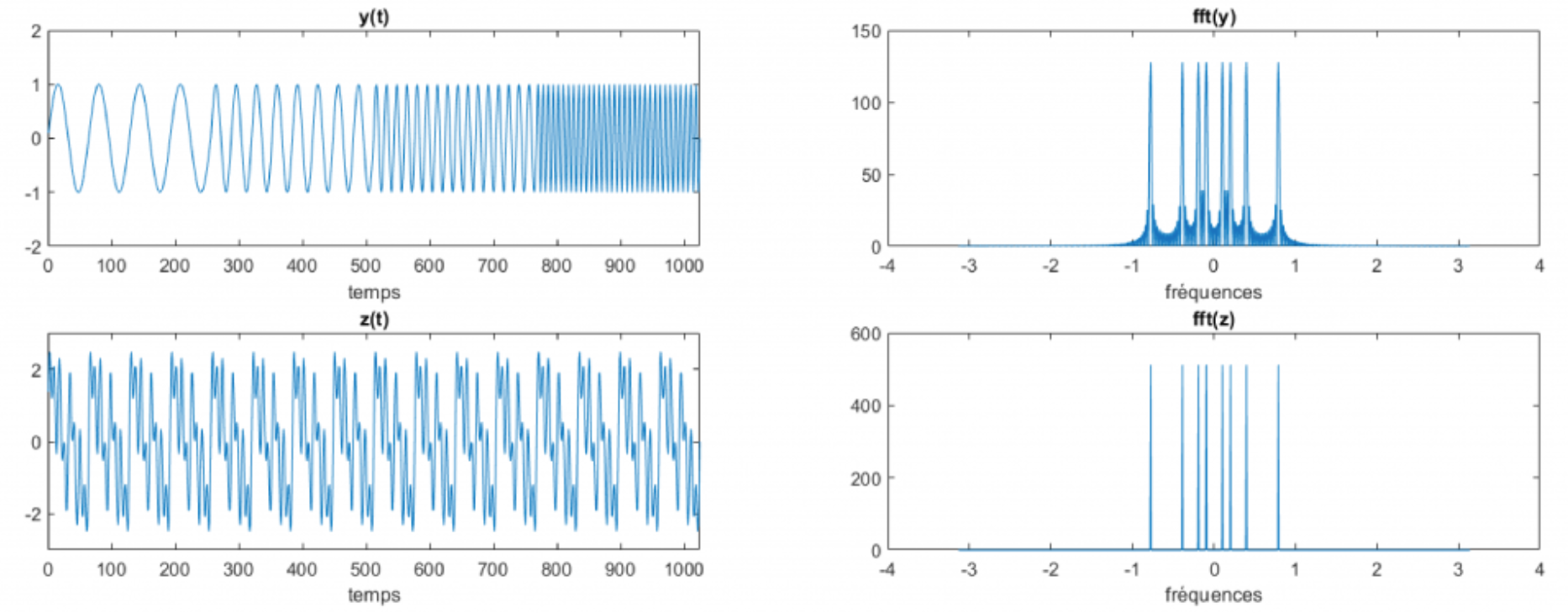

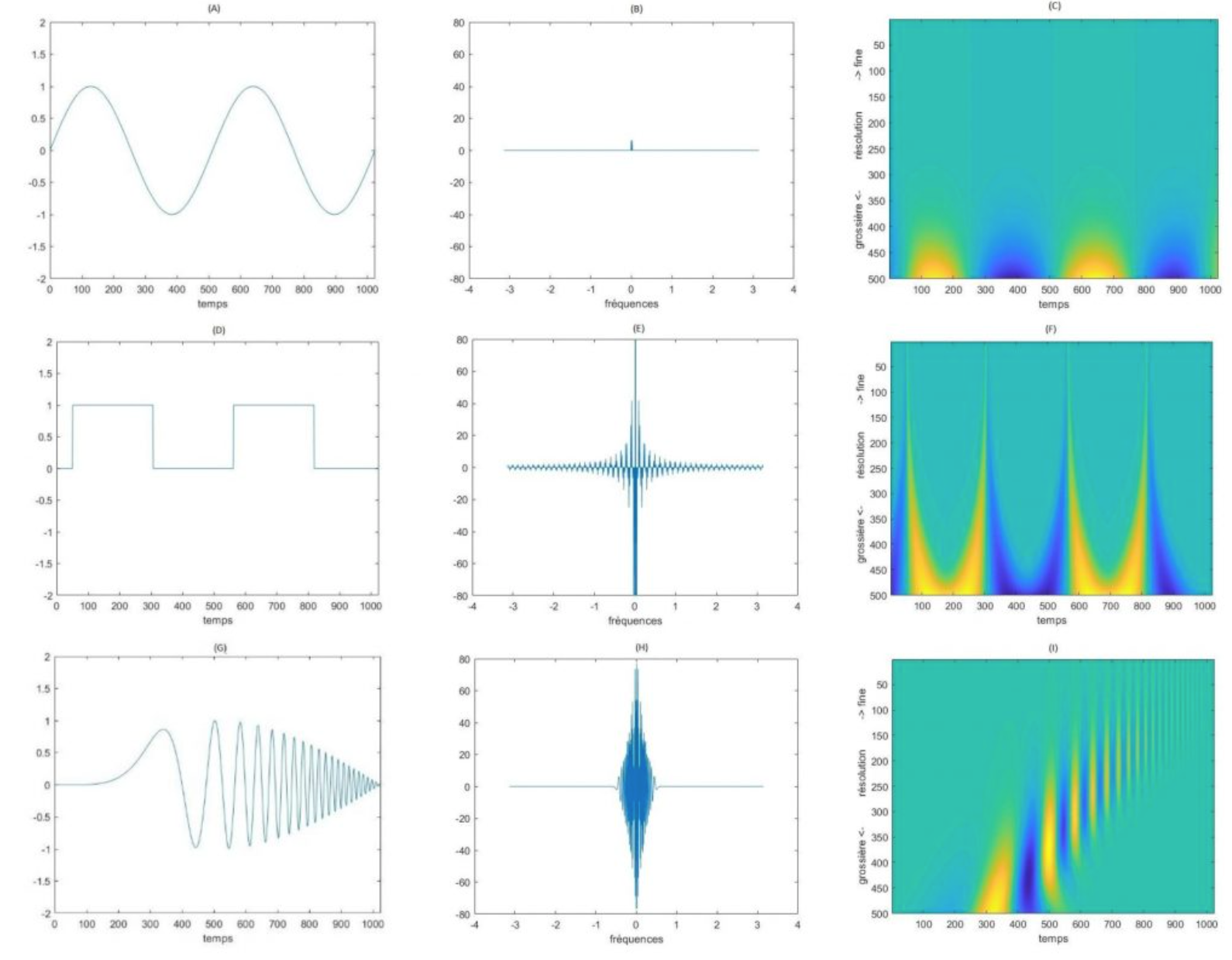
Figure 2.1. Exemple de signaux et leurs transformée de Fourier. Source https://interstices.info/.

Sur la figure Figure 2.1 on compare la transformée de Fourier associée a deux signaux temporels différents. Le premier signal (celui du haut) fait intervenir 4 fréquences différentes successives. Le second signal (celui du bas) correspond aux quatres même fréquences mais qui sont superposées. Lorsqu'on regarde les deux transformées de Fourier, on voit que les deux se rapprochent beaucoup puisqu'on retrouve les 4 fréquences dominantes. La différence vient des oscillations entre les pics. On a donc deux signaux très différent et deux transformées de Fourier assez proches. Cela vient du fait que la transformée de Fourier nous donne la distribution des fréquences sur l'ensemble du domaine temporelle. Par conséquence que les fréquences soit simultanées ou différées la transformée de Fourier le capte peu. La transformée de Fourier ignore les effets de localité spatiale ou temporelle dans un signal. La transformée en Ondelette permet de s'attaquer a ce tyoe de problème. La ou la transformée de Fourier est une transformation en fréquence, la transformée en ondelette est une transformation temps-fréquence ou espace-fréquence.

Figure 2.2. Comparaison de la transformée en ondelettes et de la transformée de Fourier sur trois signaux. Source https://interstices.info/. A gauche les signaux temporels. Au milieu: les transformées de Fourier ( fréquence en abscisse). A droite les transformées en ondelettes (temps en abscisse, résolution en ordonnées).

Avant d'introduire les mathématiques associés à la transformée en ondelettes, on va introduire des comparaison entre les deux approches sur trois signaux. Un signal classique, un signal discontinue et un signal dont la fréquence augmente en temmps. Sur la figure Figure 2.2 on voit que la tranformée de fourier pour le singal discontinues introduit bien des hautes fréquences mais ne donne aucune information sur la position des discontinuités à l'inverse de la transforméeen ondelettes qui localise la discontinuité. On remarque aussi qu'a basse résolution le transformée en ondelette du sinus et du créneau sont proches et deviennent très différents pour des résolutions fines. Si on comparer les transformées de Fourier entre les signaux 2 et 3 on retrouve des similarités contrairement à la tranformée en ondelettes et au signal d'origine. Maintenant on va introduire mathématiquement les ondelettes.

Une ondelette est une fonction représentant une petite "vague" localisée en espace (ou en temps). Le principe de la transformée en ondelettes est de représenter un signal commme une combinaison linéaire de ces ondelettes qu'on peut translater ou dilater.

Définition 2.3. Ondelette 1D.

Soit \(\Psi(x)\in L^2(\mathbb{R})\) une fonction oscillante, potentiellement complexe, appelée ondelette mère tel que \(\int_{\mathbb{R}}\Psi(x)=0\) alors une ondelette d'échelle \(s\) localisée en \(y\) est définie par:

\begin{equation*} \psi_{y,s}(x)=\frac{1}{\sqrt{\mid s\mid }}\Psi(\frac{x-y}{s}) \end{equation*}

avec \((s,y)\in \mathbb{R}^{*,+}\times \mathbb{R}\text{.}\) La transformée de fourier d'une ondelette est donnée par

\begin{equation*} \hat{\psi}_{y,s}(\omega)=\sqrt{s}\hat{\psi}(s \omega)e^{-2i\pi y \omega} \end{equation*}

Parfois on impose plus de moments nuls avec la condition \(\int_{\mathbb{R}}\mid x\mid^p\Psi(x)=0\) avec \(p\ge 1\text{.}\) Pour un signal spatial \(s\) représente l'échelle et \(y\) la position spatiale. Pour un signal temporelle \(s\) représente la fréquence et \(y\) le temps. On voit que lorsqu'on contracte une ondelette d'un facteur \(s\lt 1\) pour la localiser en espace on dilate la transformée de Fourier d'un facteur \(s\text{.}\) On ne peut donc pas construire une ondelette et plus généralement une fonction parfaitement localisée en espace et en fréquence. Cela est démontrer par le principe d'incertitude Heisenberg.

Théorème 2.4. Principe d'incertitude Heisenberg.

Soit une fonction \(f\in L^2(\mathbb{R})\) On définit la moyenne spatiale

\begin{equation*} \bar{f}=\frac{1}{\parallel f\parallel^2}\int_{-\infty}^{+\infty} x \mid f(x)\mid^2 dx \end{equation*}

et fréquentielle

\begin{equation*} \bar{\omega}=\frac{1}{2\pi \parallel f\parallel^2}\int_{-\infty}^{+\infty} \omega \mid \hat{f}(\omega)\mid^2 d\omega \end{equation*}

Les écarts autour de ses moyennes sont définies par:

\begin{equation*} \sigma_f^2=\frac{1}{\parallel f\parallel^2}\int_{-\infty}^{+\infty} (x- \bar{f})^2\mid f(x)\mid^2 dx \end{equation*}

\begin{equation*} \sigma_{\omega}^2=\frac{1}{2\pi \parallel f\parallel^2}\int_{-\infty}^{+\infty} (\omega-\bar{\omega})^2 \mid \hat{f}(\omega)\mid^2 d\omega \end{equation*}

alors on a

\begin{equation*} \sigma_f \sigma_{\omega} \ge \frac12 \end{equation*}

Preuve.

Admis

Ce résultat nous montre donc qu'une ondelette fera toujours un compromis entre localisation en fréquence et en espace (ou temps).

Définition 2.5. Transformée en ondelette continue.

Soit une fonction \(f(x)\in L^2(\mathbb{R})\) alors la transformée en ondelette de la fonction \(f(x)\) est donnée par:

\begin{equation*} W(y,s)=\int_{-\infty}^{+\infty} f(x)\bar{\psi}_{y,s}(x)dx \end{equation*}

Il existe une définition équivalente:

\begin{equation*} W(y,s)=a \int_{-\infty}^{+\infty} \hat{f}(\omega)\hat{\Psi}(s \omega) e^{2i\pi y\omega } dk \end{equation*}

avec \(\hat{f}, \hat{\Psi}\) les tranformées de Fourier de \(f, \Psi\text{.}\)

La fonction \(W(y,s)\) donne une information sur le signal \(f\) localisée en espace au point \(y\) (ou en temps) dans une voisinage de taille approximative \(s\) et une information sur \(\hat{f}\) autour de la fréquence \(\frac{1}{s}\text{.}\)

Définition 2.6. Transformée inverse en ondelette.

Soit une fonction \(W(y,s) \in L^2(\mathbb{R}\times \mathbb{R}^{*,+})\) alors la transformée inverse en ondelette de la fonction \(W(y,s)\) est donnée par:

\begin{equation*} f(x)= \int_{0}^{+\infty}\int_{-\infty}^{+\infty} \frac{W(y,s)}{s^2}\psi_{y,s}(x) dy ds \end{equation*}

avec \(\hat{f}, \hat{\Psi}\) les tranformées de Fourier de \(f, \Psi\text{.}\)

Proposition 2.7.

La transformée en ondelette continue conserve l'énergie:

\begin{equation*} \int_{-\infty}^{+\infty} \mid f(x)\mid^2 dx = \int_{0}^{+\infty}\int_{-\infty}^{+\infty} \frac{\mid W(y,s)\mid^2}{s^2} dy ds \end{equation*}

Preuve.

Admis

Exemple 2.8.

Une première ondelette mère est l'ondelette de Morley définie par

\begin{equation*} \Psi(x)=c e^{-\frac{x^2}{2}}\operatorname{cos}(5x) \end{equation*}

On peut aussi citer l'ondelette du chapeau mexicainq (dérivée seconde d'une Gaussienne):

\begin{equation*} \Psi(x)=c(1-x^2) e^{-\frac{x^2}{2}} \end{equation*}

ou l'ondelette de Haar:

\begin{equation*} \Psi(x)=\begin{cases} 1,\quad \mbox{pour } 0\ge x\gt \frac12 -1,\quad \mbox{pour } -\frac12 \ge x\gt 0 \end{cases} \end{equation*}

On va finir par introduire une transformation en ondelette ou seul le paramètre d'échelle est discritisée.

Définition 2.9. Transformée en ondelette dyadique.

Soit une fonction \(f(x)\in L^2(\mathbb{R})\) alors la transformée en ondelette dyadique de la fonction \(f(x)\) est donnée par:

\begin{equation*} W(y,2^j)=\int_{-\infty}^{+\infty} f(x)\bar{\psi}_{y,2^j}(x)dx \end{equation*}

Subsubsection 2.2.1.1 Exemples d'ondelettes

En construction

Subsection 2.2.2 Transformée en ondelette discrète et analyse multi-résolution

On va commencer par introduire la transformée en ondelette discrète avant de remarquer un coût important de l'approche. Ensuite on introduira l'analyse multirésolution qui permet de déterminer un algorithme de transformée en ondelette rapide.

En construction

Subsection 2.2.3 Ondelettes 2D

En construction