Section 6.2 Flot normalisés
On va introduire un premier modèle génératif qui construit une loi de probabilité en construisant une transformation reversible d'une loi classique.
Subsection 6.2.1 Principes des flots normalisés
Il s'agit de modèles permettant d'estimer des densités de probabilité complexes (potentiellement en grande dimension). Contrairement a d'autres méthodes qui permettent d'échantillonner la loi construite, mais ne la donnent pas explicitement les flots normalisés permettent de construire explicitement la loi. On cherche donc à approcher \(p(\boldsymbol{x})\) avec \(\boldsymbol{x} \in \mathbb{R}^d\) par une densité paramétrée \(p_{\theta}(x)\text{.}\) L'idée est la suivante: on chercher à déterminer une \textbf{transformation inversible} \(f\) tel
On suppose ici que \(\pi_{\psi}(\boldsymbol{z})\) est une distribution connue comme une loi normale multivariée ou autre de paramètre \(\psi\text{.}\) Imaginons que cette transformation est connue: comment déterminer \(p(\boldsymbol{x})\text{.}\) On rappelle que par définition des loi de probabilité
Maintenant on utilise le changement de variables dans l'intégrale de droite. Cela permet d'obtenir
En utilisant l'égalité des intégrales précédentes (car on parle de densité de probabilité) et la réécriture juste au-dessus on obtient que
On voit donc que sous réserve d'avoir une transformation inversible on peut calculer la loi \(p(\boldsymbol{x})\) à partir d'une loi connue \(\pi_{\psi}(\boldsymbol{z})\text{.}\) On voit donc qu'en construisant une transformation \(f_{\phi}\) on pourra obtenir la densité.
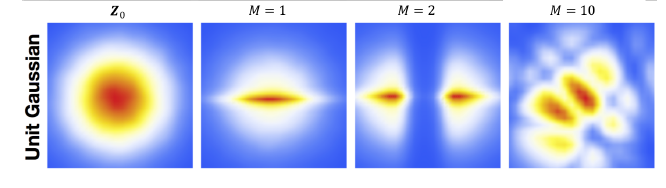
La seconde l'idée des flots normalisés est de remarque qu'en se limitant à un diffeomorphisme cela peut limiter l'expressivité du modèle \(p_{\theta}(\boldsymbol{x})\) qui va approcher \(p(\boldsymbol{x})\text{.}\) Pour cela on propose d'enchaîner une série de transformation pour obtenir un flot ( qu'on pourrait interpréter comme un flot discret issu d'une EDO). On parle de flot normalisé à cause de la présence du déterminant du jacobien. Le principe peut être vu sur l'image Figure 6.1.
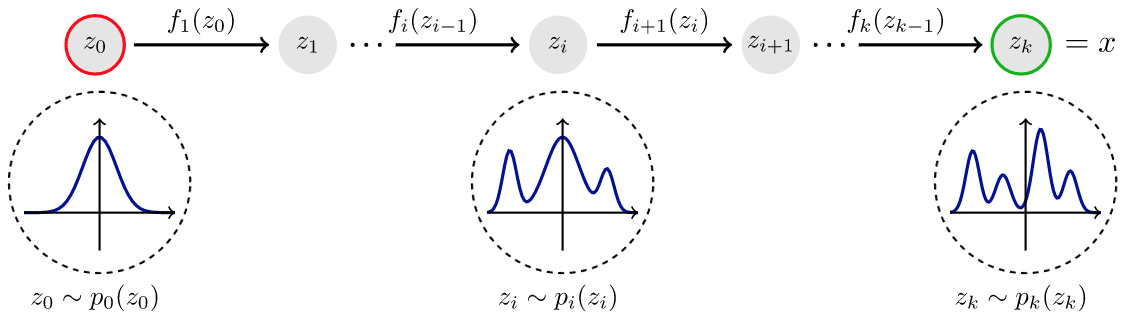
Définition 6.2. Flot normalisé.
Soit \(p_{\theta}(\boldsymbol{x})\) une densité de probabilité paramétrée. Soit \(\pi_{\psi}(\boldsymbol{z}_0)\) la densité de base. On nomme un flot normalisé la transformation:
avec \(\boldsymbol{z}_{k}=f_k((\boldsymbol{z}_{k-1})\) et \(\boldsymbol{z}_{k} \sim p_k(\boldsymbol{z}_{k})\text{.}\) Ici \(\phi\) correspond à l'ensemble des paramètres des transformations.
Proposition 6.3.
La fonction log-vraisemblance d'un flot normalisé est donnée par
Preuve.
On commence par caractériser \(p_k(\boldsymbol{z}_{k})\text{.}\) On utilise la même changement de variable que précédemment
On utilise le théorème de la fonction inverse qui dit que pour une fonction continûment différentiable la jacobienne de l'inverse est l'inverse de la jacobienne. On a donc
On utilise aussi un théorème d'algèbre linéaire qui dit que le déterminant de l'inverse d'une matrice est donné par l'inverse du déterminant de la matrice. On a donc
Ensuite on passe au \(\mathrm{log}\) et on utilise \(f_k^{-1}(\boldsymbol{z}_k)=\boldsymbol{z}_{k-1}\) pour récupérer:
Ensuite on commence a calculer:
En utilisant (6.2) on obtient:
Et en appliquant (6.2) de façon récursive on conclut.
Maintenant qu'on a défini comment calculer la vraisemblance de notre distribution issue d'un flot normalisé, on va pouvoir définir la fonction de coût à minimiser et voir comment effectuer l'apprentissage de ce type de modèle. Soit \(p^{*}(\boldsymbol{x})\) la densité qu'on cherche à obtenir et \(p_{\theta}(\boldsymbol{x})\) notre densité modélisée par un flot normalisé de paramètre \(\theta=(\psi,\phi)\text{.}\) Dans ce cas nous souhaitons résoudre:
avec \(D_{KL}\) la divergence de Kulback-Leibler. Évidemment on ne connaît \(p_{*}\) donc on doit réécrire notre problème de minimisation.
Lemme 6.4.
Soit \(p_{\theta}(\boldsymbol{x})\) une densité modélisée par un flot normalisé indexé par la transformation \(f_{\phi}(\boldsymbol{z})\) et densité \(p_{\psi}(\boldsymbol{z})\text{.}\) Dans ce cas le problème est équivalent à minimiser
avec \((\boldsymbol{x}_1,...,\boldsymbol{x}_n)\) un échantillon de \(p^{*}\text{.}\) Le gradient s'écrit de \(\mathcal{J}(\theta)\) par rapport à \(\theta\) donne
Preuve.
Minimiser la divergence de Kullback Leibler revient donc à minimiser la dernière ligne du calcul précédent sans les constantes. Maintenant il suffit d'approcher l'espérence par une espérance empirique (méthode Monte-Carlo).
Pour le gradient le calcul est immédiat, car l'espérance dépend de la loi \(p^{*}\) qui ne dépend pas de \(\theta\) par conséquent le gradient peut commuter avec l'espérance.
Subsection 6.2.2 Exemple de flots normalisés
Maintenant on va introduire des exemples de flots normalisés. Cela revient donc a proposer des transformations inversibles qui vont être plus ou moins expressives.
Subsubsection 6.2.2.1 Modèles NICE et RealNVP
Les méthodes NICE et RealNVP proposent d'appliquer des transformation qu'on pourrait dire triangulaire. C'est a dire qu'un certains nombre de dimension de notre entrée vont rester inchangés et on va appliquer une transformation sur les autres dimensions qui dépend des dimensiuon inchangées. On va commencer par introduire la méthode NICE qui est la plus simple. On se donne un entrée de \(x\in \mathbb{R}^d\) et une sortie \(y\in \mathbb{R}^d\text{.}\) La transformation utilisée dans l'approche RealNVP est donnée par avec \(m\lt d\) et \(t_{\theta}:\mathbb{R}^m\rightarrow \mathbf{d-m}\) un réseaux de neurones.
Définition 6.5. Transformation du modèle NICE.
Le deuxième avantage est le calcul rapide de la Jacobienne et du déterminant qui sera indispensable dans le calcul de la fonction coût. En effet la jacobienne est donnée par
et le déterminant est donné par \(I_d\text{.}\) Cela rend évidemment très simple le calcul de la fonction coût d'apprentissage. La méthode RealNVP va généraliser un peu la méthode NICE en prenant comme transformations non seulement des translations mais aussi des dilatations. On se donne un entrée de \(x\in \mathbb{R}^d\) et une sortie \(y\in \mathbb{R}^d\text{.}\) La transformation utilisée dans l'approche RealNVP est donnée par avec \(m\lt d\) et \(s_{\theta}:\mathbb{R}^m\rightarrow \mathbf{d-m}\text{,}\) \(t_{\theta}:\mathbb{R}^m\rightarrow \mathbf{d-m}\) des réseaux de neurones.
Définition 6.6. Transformation du modèle realNVP.
Le deuxième avantage est le calcul rapide de la Jacobienne et du déterminant qui sera indispensable dans le calcul de la fonction coût. En effet la jacobienne est donnée par:
et le déterminant est donné par:
Ce calcul est d'autant plus simple qu'il ne nécessite pas d'inverser les réseaux de neurones qui peuvent être donc arbitrairement compliqués.