Section 3.1 Rappel sur la méthode de moindres carrés
Définition 3.1. Problème des moindres carré.
Soit des matrices \(A \in \mathcal{M}_{n,k}(\mathbb{R})\text{,}\) \(b \in \mathcal{M}_{n,1}(\mathbb{R})\) et \(\theta \in \mathbb{R}^{l_2}\text{.}\) Le problème des moindres carrés associé s'écrit
Ce problème peut être vu comme l'extension du problème \(A\theta=b\) a résoudre lorsque la matrice \(A\) n'est pas inversible. Dans ce cas on cherche donc une solution qui approche au mieux le problème d'origine au sens de l'erreur euclidienne.
Lemme 3.2. Convexité et gradient.
Le problème des moindres carrés est un problème de minimisation convexe. Les solutions du problème (3.1) satisfont l'équation normale:
Preuve.
On va d'abord montrer la convexité et l'existence d'un minimum puis caractériser ce minimum.
-
Coercivité:
Soit \(\theta\in\mathbb{R}^{k}\backslash\text{Ker}(A)\text{.}\) On a
\begin{equation*} ||A\theta-b||_2^2= ||A\theta||_2^2-2\lt A\theta, b \gt +||b||_2^2\geq ||A\theta||_2^2-2||A\theta||_2.||b||_2+||b||_2^2. \end{equation*}La dernière inégalité provient de l'inégalité de Cauchy-Schwarz. Or on a
\begin{equation*} ||A\theta||_2=||A\frac{\theta}{||\theta||_2}||_2.||\theta||_2\geq \inf\left\{||Aw||_2,\ \text{avec}\ w\in\mathbb{R}^{k+1}\backslash\text{Ker}(A)\ \text{et}\ ||w||_2=1\right\}.||\theta||_2. \end{equation*}Comme \(\{w\in\mathbb{R}^{k}\backslash\text{Ker}(A)\ \text{tel que}\ ||w||_2=1\}\) est un compact et l'application \(w\in\mathbb{R}^{k}\mapsto ||Aw||_2\in\mathbb{R}\) est continue, elle est bornée et atteint ses bornes. Il existe donc \(w_0\in\mathbb{R}^{k}\backslash\text{Ker}(A)\ \text{tel que}\ ||w_0||_2=1\) et
\begin{equation*} ||Aw_0||_2=\inf\{||Aw||_2,\ \text{avec}\ w\in\mathbb{R}^{k}\backslash\text{Ker}(A)\ \text{et}\ ||w||_2=1\}. \end{equation*}donc
\begin{equation*} ||Ax||_2\geq ||Aw_0||_2.||\theta||_2. \end{equation*}Comme \(w_0\not\in\text{Ker}(A)\text{,}\) on a \(||Aw_0||_2\neq0\) et donc
\begin{equation*} ||A\theta||_2\underset{||\theta||_2\rightarrow+\infty}{\longrightarrow}+\infty. \end{equation*}Cela permet donc d'obtenir
\begin{equation*} ||A\theta||_2^2-2||A\theta||_2.||b||_2+||b||_2^2\underset{||\theta||_2\rightarrow+\infty}{\longrightarrow}+\infty. \end{equation*}Ce qui conclue la coercivité de \(J(\theta)\text{.}\)
-
Convexité sur \(\mathbb{R}^{k}\):
Soit \(t\in[0,1]\) et \(\theta_1,\theta_2\in\mathbb{R}^{k}\text{.}\) On a
\begin{align*} J(t \theta_1+(1-t) \theta_2) \amp -t J(\theta_1)-(1-t)J(\theta_2)\\ \amp =|| t A \theta_1+(1-t)A\theta_2-\underbrace{b}_{=t \theta_1+(1-t)\theta_2}||_2^2\\ \amp =t(t-1)||A\theta_1-b||_2^2-2 t(t-1)\lt A\theta_1-b, A\theta_2-b\gt +t(t-1)||A\theta_2-b||_2^2\\ \amp =t(t-1)||A\theta_1-b-(A\theta_2-b)||_2^2\\ \amp = t(t-1)||A\theta_1-A\theta_2||_2^2\\ \leq 0\text{ car }t\in[0,1]. \end{align*}Donc \(\forall t\in[0,1], \forall \theta_1,\theta_2\in\mathbb{R}^{k}\) on a
\begin{equation*} J(t \theta_1+(1-t)\theta_2)\leq t J(\theta_1)+(1-t)J(\theta_2) \end{equation*}La fonction \(J\) est bien convexe sur \(\mathbb{R}^{k+1}.\)
-
Stricte convexité sur \(\chi\text{:}\)
Si \(\theta_1,\theta_2\not\in\text{Ker}(A)\) alors \(\theta_1,\theta_2\in\chi\) (par définition de \(\chi\)). Comme \(\chi\) est un sous espace vectoriel, on a donc \(\theta_1-\theta_2\in\chi\) et ainsi \(\theta_1-\theta_2\not\in\text{Ker}(A)\text{.}\) Dans ce cas, si \(\theta_1,\theta_2\not\in\text{Ker}(A)\) et si \(t\in[0,1]\text{,}\)
\begin{equation*} J(t \theta_1+(1-t) \theta_2)-t J(\theta_1)-(1-t)J(\theta_2)=t(t-1)||A(\theta_1-\theta_2)||_2^2\lt 0 \end{equation*}car \(A(\theta_1-\theta_2)\neq 0 \text{.}\) Donc \(J\) est bien strictement convexe sur \(\chi\text{.}\)
-
Existence de l'unique minimiseur :
\(J\) est coercive et strictement convexe sur \(\chi\) elle admet donc un unique minimiseur \(\theta_2\) sur \(\chi\) (le théorème ..." toute fonction coercive et strictement convexe sur un espace vectoriel \(E\in\mathbb{R}^{k+1}\) admet un unique minimiseur sur \(E\text{.}\)").
Soit \(\mathcal{S}\) l'ensemble des solutions au problème des moindres carrés (c'est-à-dire l'ensemble des minimiseurs de \(J\) sur \(\mathbb{R}^{k})\text{.}\) Montrons que \(\mathcal{S}=\{\theta_2+\omega,\ \text{avec}\ \omega\in\text{Ker}(A)\}\text{.}\) On montre d'abord la 1ère première inclusion.
Soit \(\theta_0\in\mathbb{R}^{k}\) alors \(\theta_0\) se décompose en \(\theta_0=\mu_0+\omega\) avec \(\mu_0\in\chi\) et \(\omega\in\text{Ker}(A)\)> (par définition de \(\chi\)). Donc
\begin{equation*} J(\theta_0)=||A\mu_0+A\omega-b||_2^2=||A\mu_0-b||_2^2=J(\mu_0)\geq J(\theta_2) \end{equation*}car \(\theta_2\) est le minimiseur sur \(\chi\) et \(\mu_0\in\chi\text{.}\) Or, pour tout \(\omega\in\text{Ker}(A)\text{,}\) on a
\begin{equation*} J(\theta_2+\omega)=||A\theta_2+A\omega-b||_2^2=||A\theta_2-b||_2^2=J(\theta_2) \end{equation*}Donc pour tout \(\theta_0\in\mathbb{R}^{k}\) et tout \(\omega\in\text{Ker}(A)\text{,}\) on a \(J(\theta_0)\geq J(\theta_2)=J(\theta_2+\omega)\text{.}\) Donc \(\theta_2+\omega\) est bien un minimiseur de \(J\) sur \(\mathbb{R}^{k}.\) Ainsi \(\{\theta_2+\omega,\ \text{avec}\ \omega\in\text{Ker}(A)\}\subset\mathcal{S}.\)
Maintenant on montre la deuxième inclusion: Soit \(\widehat{x}\) une solution au problème des moindres carrés. Alors \(\widehat{x}\) est un minimiseur de \(J\) sur \(\mathbb{R}^{k}\) (ce n'est pas \(\theta_2\) car \(\theta_2\) est le minimiseur sur \(\chi\)). On a \(J(\widehat{\theta})\leq J(z)\) pour tout \(z\in\mathbb{R}^{k}\) donc entre autres pour tout \(z\in\chi\text{.}\) Or \(\widehat{\theta}\) se décompose en \(\widehat{\theta}=\widehat{\mu}+\widehat{\omega}\) avec \(\widehat{\mu}\in\chi\) et \(\widehat{\omega}\in\text{Ker}(A)\text{.}\) Comme précédemment, on a \(J(\widehat{\theta})=J(\widehat{\mu})\) donc \(J(\widehat{\mu})\leq J(z)\text{,}\) pour tout \(z\in\chi\text{.}\) Ainsi \(\widehat{\mu}=\theta_2\) par unicité du minimiseur sur \(\chi\text{.}\) Donc
\begin{equation*} \widehat{\theta}=\theta_2+\widehat{\omega}\in\{\theta_2+\omega,\ \text{avec}\ \omega\in\text{Ker}(A)\}. \end{equation*}On a donc
\begin{equation*} \mathcal{S}\subset\{x\theta_2+\omega,\ \text{avec}\ \omega\in\text{Ker}(A)\}. \end{equation*} -
Calcul du gradient:
\begin{equation*} \nabla_{\theta} \mathcal{J}(\theta)=0 \end{equation*}On calcul le gradient
\begin{align*} \mathcal{J}(\theta+h) \amp =\langle A(\theta+h)-b,A(\theta+h)-b\rangle\\ \amp=\mathcal{J}(\theta)+2\langle A \theta -b,A h\rangle+o(h)\\ \amp =\mathcal{J}(\theta)+\langle 2A^t(A\theta-b),h\rangle+o(h) \end{align*}Donc
\begin{equation*} \nabla \mathcal{J}_r(x)h=\lim\limits_{\varepsilon\rightarrow 0}\frac{\mathcal{J}_r(\theta+\varepsilon h)-\mathcal{J}(\theta)}{\varepsilon}=\langle 2A^t(A \theta-b),h\rangle \end{equation*}et ainsi
\begin{equation*} \nabla_{\theta} \mathcal{J}(\theta) =0 \Longleftrightarrow 2A^t(A\theta - b)=0 \end{equation*} -
Solution de l'équation normale:
\(J\) est différentiable et \(\nabla J(\theta)=2(A^TA\theta-A^Tb)\text{.}\) Montrons que \(\theta\) minimise \(J\) sur \(\mathbb{R}^{k}\text{,}\) \(\Leftrightarrow A^TA\theta=A^Tb\text{.}\)
-
Sens \(\Rightarrow\text{:}\)
Si \(\theta\) est un minimiseur de \(J\) sur \(\mathbb{R}^{k}\) alors \(\nabla J(\theta)=0\) (égalité d'Euler) donc \(A^TA\theta=A^Tb\text{.}\)
-
Sens \(\Leftarrow\text{:}\)
Si \(A^TA\theta=A^Tb\text{,}\) alors \(\nabla J(\theta)=0\text{.}\) Comme \(J\) est convexe sur \(\mathbb{R}^{k}\) qui est un ouvert, d'après l'indice de l'énoncé, la réciproque de l'égalité d'Euler a lieu et \(\theta\) est bien un minimiseur de \(J\) sur \(\mathbb{R}^{k}\text{.}\)
-
Lemme 3.3. Equation normale.
Soit une matrice \(A\) tel que \(n \gt k \text{.}\) Si la matrice \(A\) est de rang maximal, il existe une unique solution du problème des moindres carrés est donnée par
La matrice \(A^+\) est appelée le pseudo-inverse de Moore-Penrose.
Preuve.
On a \(\lt \theta, A^TA\theta \gt = \lt A\theta, A\theta \gt=||A\theta||^2_2\text{.}\) Donc \(A^TA\theta=0\Leftrightarrow A\theta=0\text{.}\) Cela permet d'obtenir \(\text{Ker}(A^TA)=\text{Ker}(A)\text{.}\)
Par le théorème du rang, on a \(k=rang(A)+\text{dim}(\text{Ker}(A))\) et \(k=rang(A^TA)+\text{dim}(\text{Ker}(A^TA))\text{.}\) Donc \(rang(A)=rang(A^TA).\) Par définition le rang maximal est donné par \(rang(A)=\operatorname{min}(n,k)=k\text{.}\) Ainsi, si \(rang(A)=k\text{,}\) alors \(rang(A^TA)=k\text{.}\) Or \(A^TA\) est une matrice carrée de taille \((k)\times(k)\) donc si son rang vaut \(k\text{,}\) c'est qu'elle est inversible.
Il existe donc un unique vecteur \(\widehat{\theta}\) qui soit solution de l'équation normale \(A^TA\widehat{\theta}=A^Tb.\)
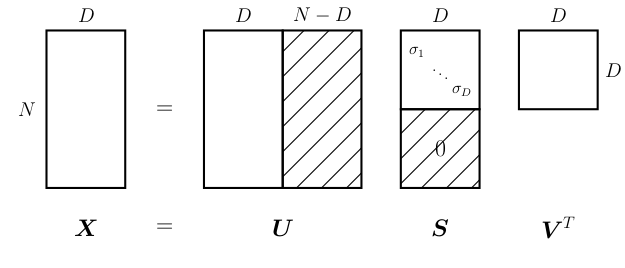
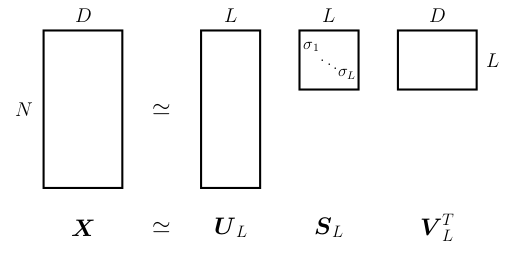
Pour finir on va introduire un second outils la décomposition en valeurs singulière. Il s'agit d'une généralisation de la diagonalisation aux matrices non carrés. Elle est très utilisée dans ces problème du type moindre carrés. Soit \(A\in\mathcal{M}_{n,d}(\mathbb{R})\) de rang \(r>0\text{.}\) Il existe \(U_r\in\mathcal{M}_{n,r}(\mathbb{R})\) et \(V_r\in\mathcal{M}_{d, r}(\mathbb{R})\text{,}\) orthogonales, tel que avec \((\sigma_1,...\sigma_r)\) les valeurs singulières données par \(\sigma_i=\sqrt{\lambda_i}, \quad \forall i\leq r\) avec \(\lambda_i\) les valeurs propres de \(A^t A\) et \(V_r\) la matrice des \(r\) vecteurs propres de \(A^t A\) associées à des valeurs propres strictement positive. On peut donc écrire la matrice \(A\) sous la forme Soit la troncature: avec \(m\leq r\) est la meilleur approximation de \(A\) (au sens de la norme de Frobinus) parmis les matrices de rang \(m\text{.}\) Cela equivaut à:
Théorème 3.4. Théorème de la SVD.
Preuve.
Comme \(A^t A\) est symétrique réelle, elle est diagonalisable dans une base de vecteurs propres orthogonaux. On a donc:
On pose \(V_r\in\mathcal{M}_{d,r}(\mathbb{R})\) la matrice formée des \(r\) premières colonnes de \(V\) avec
On a alors \(V_r^t V_r = I_r\) et \(V_rV_r^t +**^T=I_{p}\) (car \(V^t V=VV^t =I_{d}\)). On note \(\lambda_i\) les valeurs propres de \(A^t A\text{,}\) puisque le rang de \(A\) vaut \(r\) on a \(d-r\) valeurs propres nulles, ainsi:
En notant \(\Sigma=\text{diag}(\sqrt{\lambda_1}, ..., \sqrt{\lambda_r})\in\mathcal{M}_{r, r}(\mathbb{R})\text{,}\) on a \(V_r^t A^t A V_r= \Sigma^2\) et \(A^*=0\text{.}\) On souhaite maintenant se ramener à \(A\text{.}\) On remarque que
donc en posant \(U_r= A V_r\Sigma^{-1} \in \mathcal{M}_{n,r}(\mathbb{R})\text{,}\) on a
mais aussi
Il nous reste à construire la matrice \(U\) carrée à partir de \(U_r\text{.}\) Comme \(U_r^t U_r = I_r\text{,}\) les colonnes de \(U_r\) forment une famille orthogonale qu'on peut compléter en base orthonormale. On pose
La concaténation en colonne des vecteurs de cette nouvelle base. On a ainsi \(U^t U=I_n=UU^t\) (car \(U\) est carrée). Donc